Nonlinear aerodynamics of airfoils at low Reynolds number and its prediction model
-
摘要:
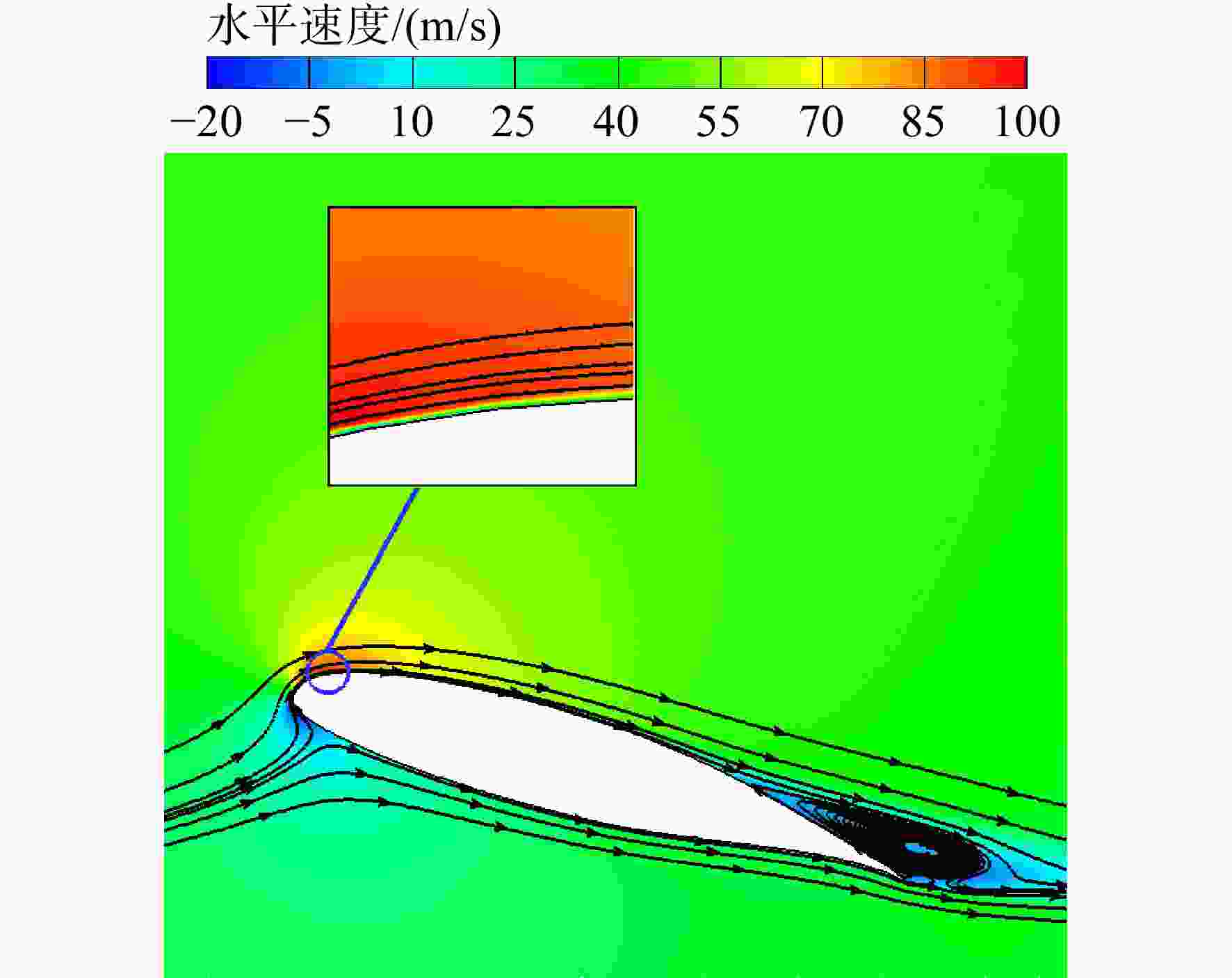
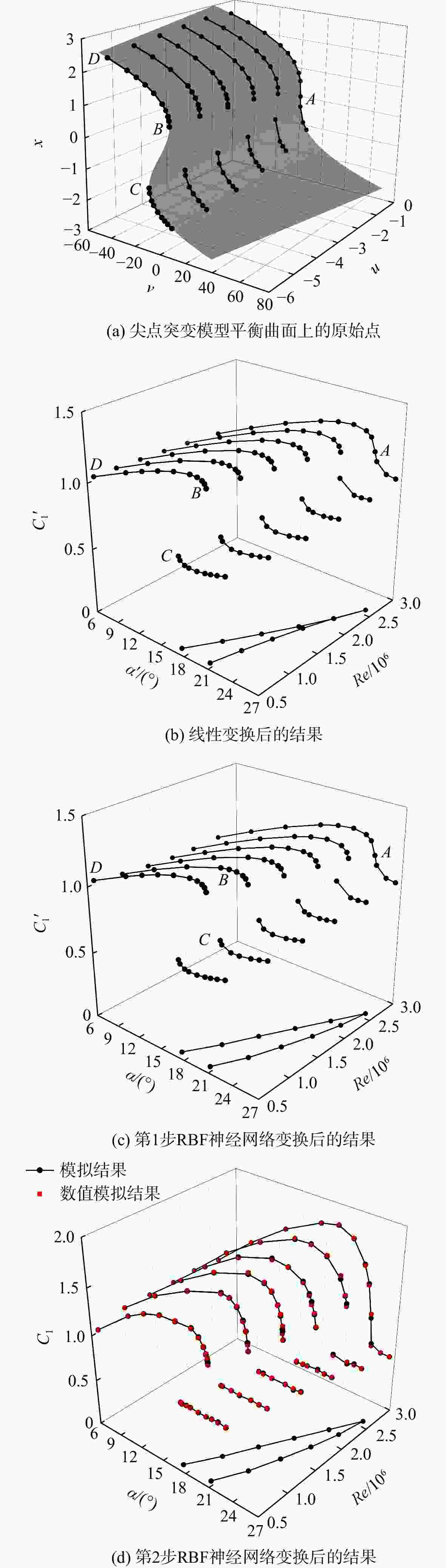
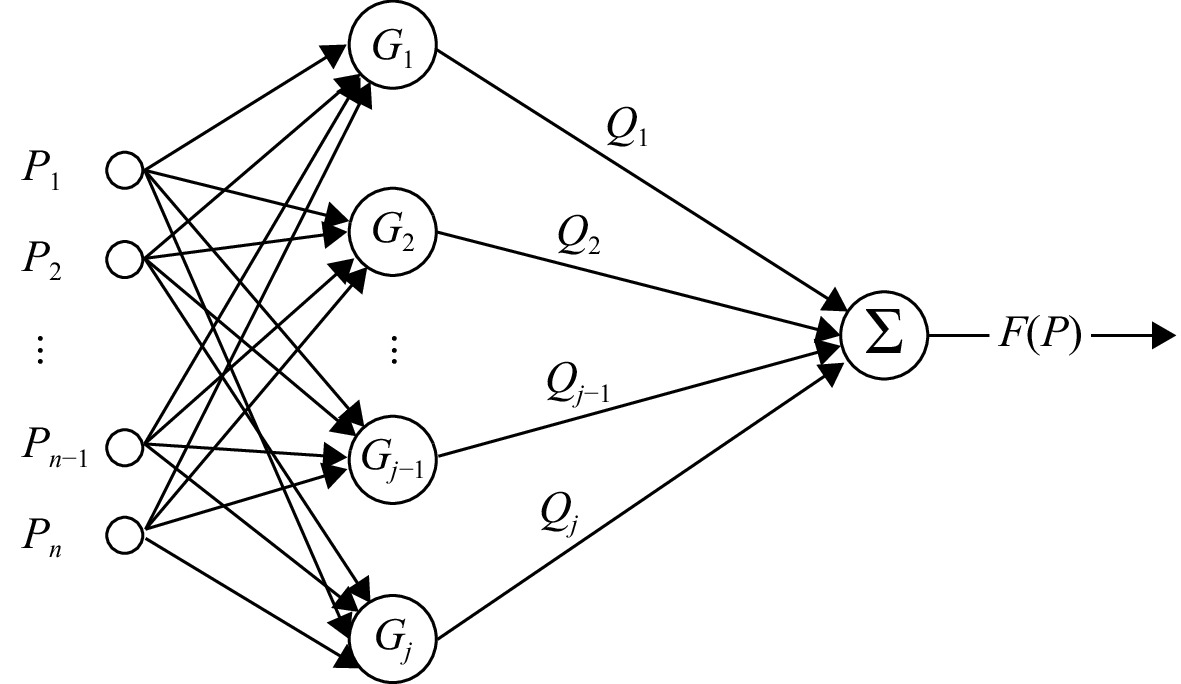
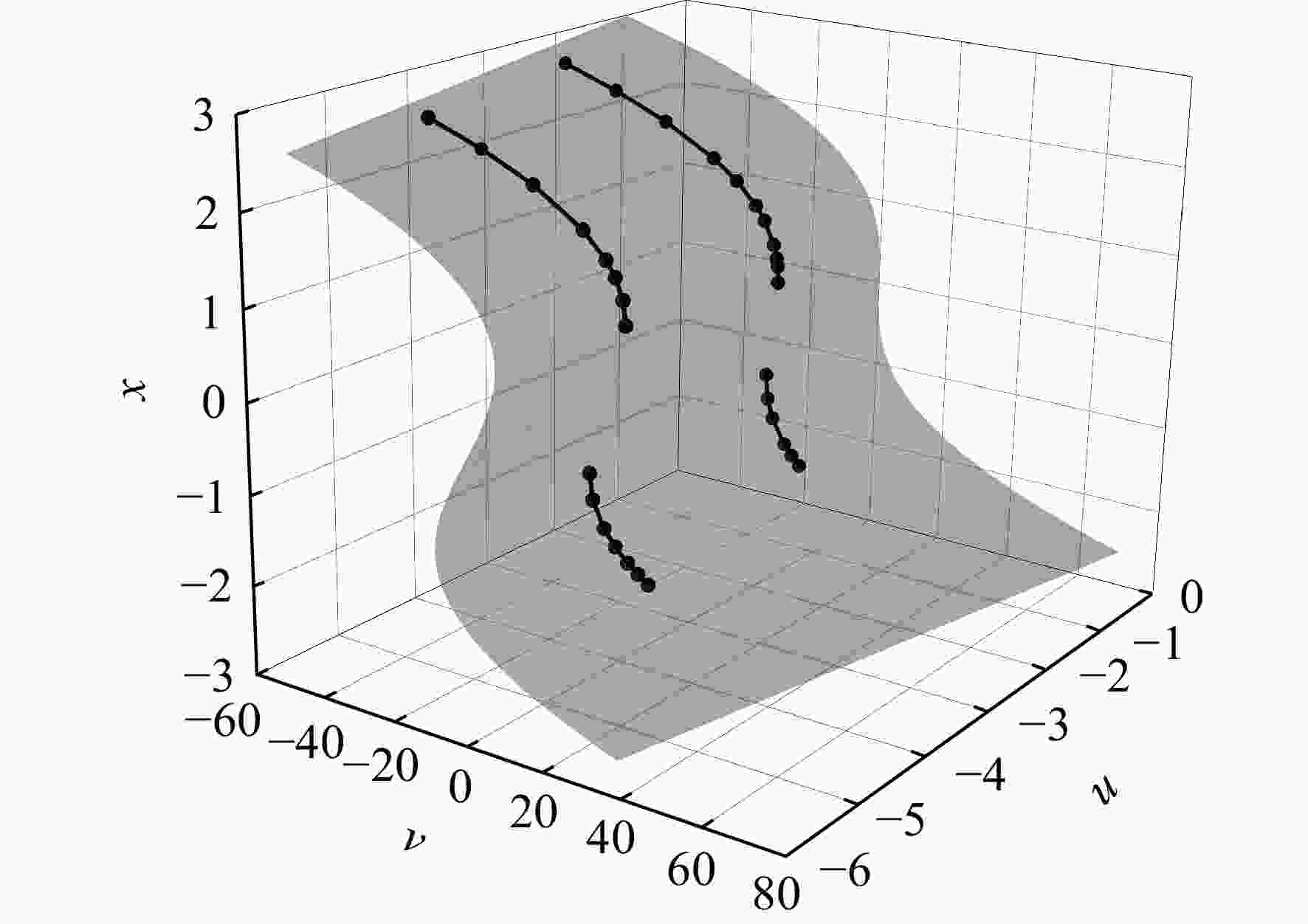
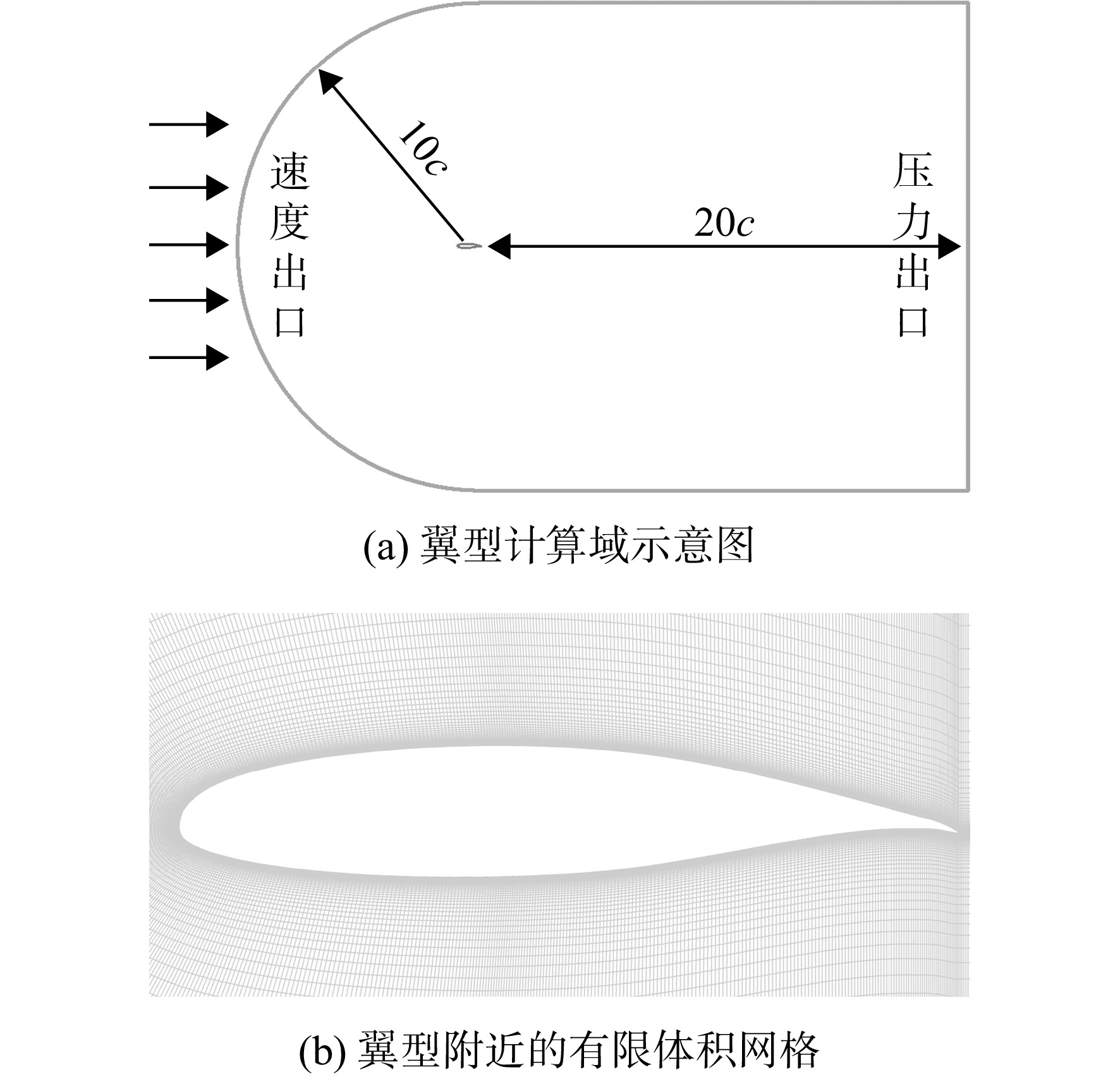
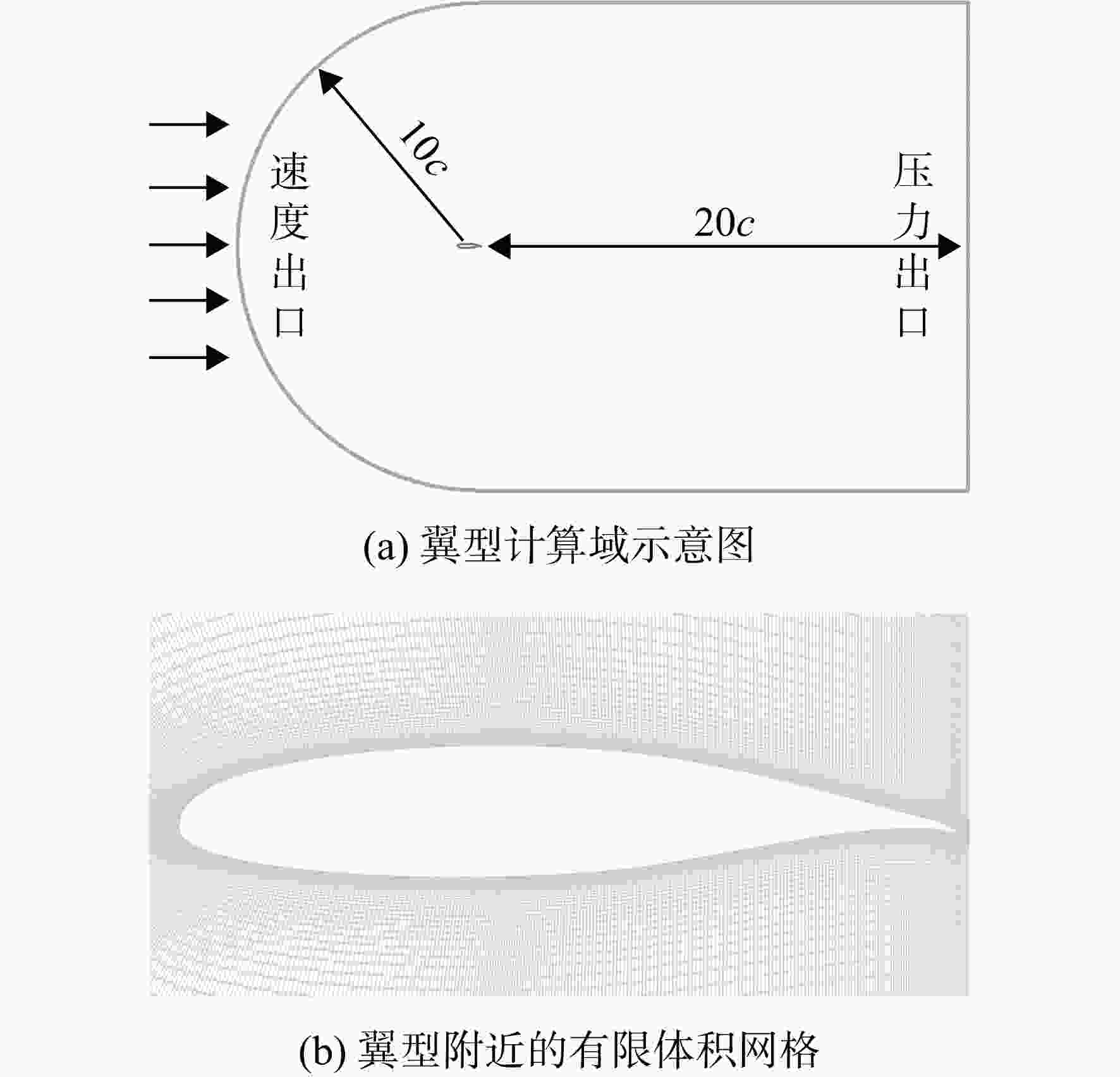
以GA（W）-1翼型为研究对象，通过数值模拟的方法探究了雷诺数对翼型气动特性的影响规律及物理机制，结果显示：翼型在低雷诺数工况下具有突变性、迟滞性等强烈的非线性气动特性，且迟滞环的尺寸随着雷诺数的增大而逐渐减小直到最终消失，翼型前缘分离泡的破碎及该过程的不可逆性是非线性气动特性产生的物理根源。翼型在不同雷诺数工况下的非线性气动特性与尖点突变模型在空间拓扑上具有相似性，于是基于拓扑不变原理，通过发展高精度的拓扑映射方法，构建了尖点突变模型的平衡曲面与翼型非线性气动特性之间的拓扑映射关系，从而利用尖点突变模型的平衡曲面去预测低雷诺数下翼型的非线性气动特性，模型预测误差在5%以内。
Abstract:Taking the GA(W)-1 airfoil as the research object, the influence law and physical mechanism of the Reynolds number on the aerodynamic characteristics of the airfoil through numerical simulation were investigated. The results showed that the airfoil had strong nonlinear aerodynamic characteristics such as catastrophe and hysteresis under low Reynolds number conditions, and the size of the hysteresis loop gradually decreased and even disappeared with the increase of Reynolds number. The breakup of the separation bubble at the leading edge of the airfoil and the irreversibility of this process constituted the physical origins of the nonlinear aerodynamic characteristics. The nonlinear aerodynamic characteristics of the airfoil under different Reynolds numbers were in accordance with the topological features of the cusp catastrophic model. Therefore, based on the principle of topology invariance, a high-precision topology mapping method was developed to establish the mapping relationship between cusp catastrophic model and nonlinear characteristics of the airfoil, then the nonlinear aerodynamic characteristics of the airfoil at low Reynolds number were successfully predicted by the equilibrium surface of the cusp catastrophic model, and the model error was less than 5%.
-
Key words:
- airfoil /
- low Reynolds number /
- nonlinear aerodynamics /
- cusp catastrophic model /
- prediction model
-
图 3 翼型在不同雷诺数工况下的升力特性
Figure 3. Lift characteristics of the airfoil at different Reynolds numbers
图 4 翼型平均流场的流线和水平速度分布（
$Re{\text{ = }}0.6 \times {10^6}$ 、$\alpha {\text{ = }}18{\text{°}} $ ）Figure 4. Streamline and horizontal velocity distributions of the mean flow field of the airfoil （
$Re{\text{ = }}0.6 \times {10^6}$ ,$\alpha {\text{ = }}18{\text{°}} $ ）
图 5 翼型平均流场的流线和水平速度分布（
$Re{\text{ = }}2.6 \times {10^6}$ 、$\alpha {\text{ = }}18{\text{°}} $ ）Figure 5. Streamline and horizontal velocity distributions of the mean flow field of the airfoil （
$Re{\text{ = }}2.6 \times {10^6}$ ，$\alpha {\text{ = }}18{\text{°}} $ ）
图 6 尖点突变模型平衡曲面的空间拓扑
Figure 6. Topological structure of the equilibrium surfaces for cusp catastrophic model
图 9 尖点突变模型平衡曲面上的原始点
Figure 9. Original points on the equilibrium surface of the cusp catastrophic model
-
[1] MUELLER T J. The influence of laminar separation and transition on low Reynolds number airfoil hysteresis[J]. Journal of Aircraft,1985,22(9): 763-770. doi: 10.2514/3.45199 [2] POHLEN L J,MUELLER T J. Boundary layer characteristics of the Miley airfoil at low Reynolds numbers[J]. Journal of Aircraft,1984,21(9): 658-664. doi: 10.2514/3.45011 [3] SELIG M, GUGLIELMO J, BROERN A, et al. Experiments on airfoils at low Reynolds numbers[R]. AIAA 1996-62, 1996. [4] MARCHMAN J F III,SUMANTRAN V,SCHAEFER C G. Acoustic and turbulence influences on stall hysteresis[J]. AIAA Journal,1987,25(1): 50-51. doi: 10.2514/3.9578 [5] BIBER K. Physical aspects of stall hysteresis on an airfoil with slotted flap[R]. AIAA 1995-440, 1995. [6] LIU Yan,LI Kailun,ZHANG Jiazhong,et al. Numerical bifurcation analysis of static stall of airfoil and dynamic stall under unsteady perturbation[J]. Communications in Nonlinear Science and Numerical Simulation,2012,17(8): 3427-3434. doi: 10.1016/j.cnsns.2011.12.007 [7] LEUNG A Y T,GUO Zhongjin. Residue harmonic balance for two-degree-of-freedom airfoils with cubic structural nonlinearity[J]. AIAA Journal,2011,49(12): 2607-2615. doi: 10.2514/1.J050800 [8] BENNET D J,MCINNES C R. Pattern transition in spacecraft formation flying using bifurcating potential fields[J]. Aerospace Science and Technology,2012,23(1): 250-262. doi: 10.1016/j.ast.2011.07.013 [9] DING Qian,WANG Dongli. The flutter of an airfoil with cubic structural and aerodynamic non-linearities[J]. Aerospace Science and Technology,2006,10(5): 427-434. doi: 10.1016/j.ast.2006.03.005 [10] LIU Liping,DOWELL E H. The secondary bifurcation of an aeroelastic airfoil motion: effect of high harmonics[J]. Nonlinear Dynamics,2004,37(1): 31-49. doi: 10.1023/B:NODY.0000040033.85421.4d [11] MAQSOOD A,GO T H. Multiple time scale analysis of aircraft longitudinal dynamics with aerodynamic vectoring[J]. Nonlinear Dynamics,2012,69(3): 731-742. doi: 10.1007/s11071-011-0300-3 [12] THOM R. Mathematical models of morphogenesis[M]. Chichester, UK: Ellis Horwood, 1983. [13] 李志平,张鹏,李秋实. 低速轴流压气机旋转失速边界的模型描述[J]. 航空动力学报,2017,32(3): 519-527. doi: 10.13224/j.cnki.jasp.2017.03.002LI Zhiping,ZHANG Peng,LI Qiushi. Model description of rotating stall boundary in low-speed axial compressor[J]. Journal of Aerospace Power,2017,32(3): 519-527. (in Chinese) doi: 10.13224/j.cnki.jasp.2017.03.002 [14] CUI Tao,LÜ Zhong,YU Daren. Multistability and complex routes of supersonic inlet start/unstart[J]. Journal of Propulsion and Power,2011,27(6): 1204-1217. doi: 10.2514/1.B34235 [15] BAO Jiusheng,YIN Yan,LU Yuhao,et al. A cusp catastrophe model for the friction catastrophe of mine brake material in continuous repeated brakings[J]. Proceedings of the Institution of Mechanical Engineers: Part J Journal of Engineering Tribology,2013,227(10): 1150-1156. doi: 10.1177/1350650113482825 [16] LI Zhiping,ZHANG Peng,PAN Tianyu,et al. Catastrophe-theory-based modeling of airfoil-stall boundary at low Reynolds numbers[J]. AIAA Journal,2018,56(1): 36-45. doi: 10.2514/1.J056048 [17] MENTER F R,LANGTRY R B,LIKKI S R,et al. A correlation-based transition model using local variables: Part Ⅰ model formulation[J]. Journal of Turbomachinery,2006,128(3): 413-422. doi: 10.1115/1.2184352 [18] GHASEMI E,MCELIGOT D M,NOLAN K P,et al. Entropy generation in a transitional boundary layer region under the influence of freestream turbulence using transitional RANS models and DNS[J]. International Communications in Heat and Mass Transfer,2013,41: 10-16. doi: 10.1016/j.icheatmasstransfer.2012.11.005 [19] WANG Shengyi,INGHAM D B,MA Lin,et al. Numerical investigations on dynamic stall of low Reynolds number flow around oscillating airfoils[J]. Computers and Fluids,2010,39(9): 1529-1541. doi: 10.1016/j.compfluid.2010.05.004 [20] HU Hui,YANG Zifeng,IGARASHI H. Aerodynamic hysteresis of a low-Reynolds-number airfoil[J]. Journal of Aircraft,2007,44(6): 2083-2086. doi: 10.2514/1.32662 [21] WHITNEY H. On singularities of mappings of euclidean spaces: Ⅰ mappings of the plane into the plane[J]. The Annals of Mathematics,1955,62(3): 374-410. doi: 10.2307/1970070 [22] MUSAVI M T,AHMED W,CHAN K H,et al. On the training of radial basis function classifiers[J]. Neural Networks,1992,5(4): 595-603. doi: 10.1016/S0893-6080(05)80038-3 -
下载:
点击查看大图
计量
- 文章访问数: 160
- HTML浏览量: 53
- PDF量: 45
- 被引次数: 0