Fast automatic correction method for component characteristics of the identification dynamic model of VCE
-
摘要:
为实现模型部件特性快速自动修正的工程需求，提出一种针对身份证模型部件特性的增强型自动修正策略，以稳态试车数据为输入，依据可测传感器组合，分析选取合适的特性修正系数组合，并耦合个体试车数据对共同工作方程进行设计，利用多点修模的双环策略快速自动修正部件特性，实现某型变循环发动机身份证模型的快速自动修正。采取逆流路扰动及Newton-Raphson迭代阻尼系数自调整法和特性图外插保护逻辑等方法提高算法的运行速率和稳定性。仿真结果表明：修正后模型输出最大误差小于0.1%，在2.10 GHz处理器的计算机上单、双涵道模式与常规部件级模型相比，耗时减少98.6%以上，所修正后模型可用于控制律设计以及为确定发动机当前真实状态提供参考。
-
关键词:
- 变循环发动机 /
- 增强型模型快速自动修正策略 /
- 多点修模的双环策略 /
- Newton-Raphson迭代阻尼系数自调整 /
- 身份证动态模型
Abstract:To realize the engineering requirement for fast automatic correction of model component characteristics, an enhanced automatic correction strategy of the identification model component characteristics was proposed. Taking steady-state test data as input, the designed correction strategy allowed to analyze and select suitable characteristic correction coefficient combinations based on sensor measurements. The proposed method also coupled individual rig test data of engine to design the equilibrium equations, and used the double-loop strategy of multi-point model correction to quickly and automatically correct component characteristics. Finally, the fast automatic correction of the identification model of a certain variable cycle engine was realized. The inverse flow path disturbance, damping coefficient self-adjustment method of Newton-Raphson method and characteristic map interpolation protection logic were adopted to improve the operation rate and stability of the algorithm. The simulation results showed that the maximum output error of the corrected model was less than 0.1%, and the consuming-time was reduced by more than 98.6% compared with the common component-level model, which was simulated in single and double bypass modes on a computation with 2.10 GHz processor. The corrected model can be used for control law design and also provide a reference for determining the current real state of the engine.
-
变循环发动机（VCE）部件级模型是VCE设计方案优化、控制算法设计和性能故障诊断等研发过程的重要工具[1]。精度较差的VCE部件级模型会导致控制算法控制效果降低，故障诊断出现误诊漏诊等问题[2]，因此高精度的发动机模型对于节省研发成本[3]，提高控制算法设计质量等有较高的工程应用价值[4-5]。然而，一个固定的发动机模型很难匹配一个型号的全部发动机或者一台发动机在全服役期内不同阶段的状态，这是因为发动机模型和发动机实际传感器的量测值总会存在误差，这主要有以下3个原因：①发动机在装配时的装配误差及零件制造公差等导致的误差[6]；②发动机长期服役性能退化导致的传感器参数的变化[7]；③发动机部件特性在整机运行和单一部件运行时获取的特性图有所差异导致的误差[8]。
为了获取较高精度的发动机模型以用于发动机控制律设计等任务，能够有一种快速的模型修正方法就较为重要。目前常见的发动机模型的修正方法主要有以下3种：①人工手动模型修正；②采用寻优算法进行模型自动修正；③采用非线性求解算法进行模型修正。
采用人工手动模型修正的方法，主要是由富有经验的专业修模人员通过对特性修正系数及总压总温恢复系数等可调参数进行手动调整。俞明帅[9]通过对发动机部件参数及总温、总压恢复系数对模型输出参数的影响，提出了根据试车数据与模型的误差，对特性图的流量、效率、压比和转速特性进行移动的一种手调方法，同时提出了对部分截面总温和总压恢复系数调整的方法，经过4次修正后，将4个传感器误差调整至1%以内。钟文城等[10]对特性图修正增加了第三维度，让特性线按照特性线的均值旋转，修正后模型稳态平均误差从0.901%降至0.344%。人工手动修模可以根据长期修模经验对发动机的各特性图进行修正，可以较好地符合研究所的具体需求，但是这需要耗费较大的时间且需要修模人员需具有较丰富的经验。
采用寻优算法进行模型修正的方法，主要是利用寻优算法进行模型自动修正。郑斐华[11]利用粒子群算法对发动机部件级模型中的部分旋转部件特性进行修正，最终使得模型主要输出参数的误差小于7%。潘鹏飞[12]利用遗传算法对模型的设计点和非设计点进行修正，最终将部件级模型的输出误差修正至2%以内。 Li、Tsoutsanis等[13-14]将部件级模型的特性线看作椭圆曲线，利用寻优算法对椭圆长短轴、焦点和旋转角等参数进行寻优，最终主要输出参数误差均小于4%。Tsoutsanis等[15]对压缩部件的特性修正系数采取正弦函数，对涡轮部件的特性修正系数采取四次多项式，并成功将修正后模型应用于参数预测工程任务。王军等[16]先利用条件数选取修正系数，再采用最小二乘法对修正系数进行求解。利用寻优算法进行模型修正可以考虑到较多参数对模型输出的影响，但在某些情况下不一定能保证全部输出的精度符合指标。
采用非线性求解器进行模型修正的方法，主要是将模型输出与试车数据的残差作为方程，利用不同的非线性求解算法对部分特性修正系数进行求解。Visser等[17]和潘阳[18]将模型输出与试车数据残差放入模型中，潘阳在涡轴发动机模型上进行应用，对3个特性修正参数进行修正的情况下，利用非线性求解器实现了模型输出精度小于0.33%，耗时150 ms。陈玉春等[19]针对Newton-Raphson（NR）迭代法对初猜值依赖度高、稳定性差等问题，设计了变步长牛顿法，较大幅度地改善了模型稳定性。段守付等[20]采取加权函数法对特性图进行修正，更新后模型最大误差小于0.5%。俞明帅[9]采取双层NR迭代法，对4个修正系数进行求解，最终各输出误差均小于设置的收敛精度0.5%。鲁峰、陆军等[21-22]采用卡尔曼滤波器作为非线性求解器求解特性修正系数，并在涡扇发动机模型上进行仿真，各可测输出误差均小于0.5%。利用非线性求解器具有速度快，精度高的特点，但由于可测传感器数量限制，可选取的修正系数数量也有限制，因此修正系数如何选取是需要重点考虑的问题。不仅要使得特性修正系数的解唯一，且要能合理表示特性图的主要变化因素。
上述模型修正算法应用于VCE上主要有以下3点困难：
1） 若采取人工修模，虽然修模人员可以和需求单位进行良好沟通，按照需求单位的某些特殊需求进行针对性修模，但是由于现在的工业发展，同型号发动机量产速度极快，依靠人力进行模型修正，耗时较高，人力成本也较高[23]。
2） 若采取基于粒子群等寻优算法进行寻优，虽然在试车数据与模型误差较小时，往往具有较好的修正效果，但在初始误差较大时，由于待修正系数和传感器数量的增多，不一定可以保证在多个试车点下模型输出精度都能达到工程指标要求，有可能陷入局部最优[24]。
3） 若采用基于非线性求解器的方法，虽然可以在较短时间内对主要特性参数进行合理修正，但由于航空发动机的工作环境恶劣，可测传感器的数量一般少于待修正参数的数量，因此如何根据可测传感器选取合适的特性修正系数需要重点分析[25]。
因此本文针对VCE对快速自动模型修正方法的工程需求，根据VCE可测传感器的数量和类型，分析选取了VCE的特性修正系数组合，设计了耦合发动机个体试车值对共同工作方程进行设计，并利用NR迭代法求解特性修正系数的方法，同时以逆流路法和变阻尼系数NR迭代法提升了模型的运行时间和稳定度，使得代码的成功率和运行速度进一步提升，最后采取多工作状态一致修正方法对特性图进行修正，设计了VCE身份证模型自动修正方法，更符合工程的实际应用需求。
1. VCE特性修正系数选取
1.1 VCE原理简述
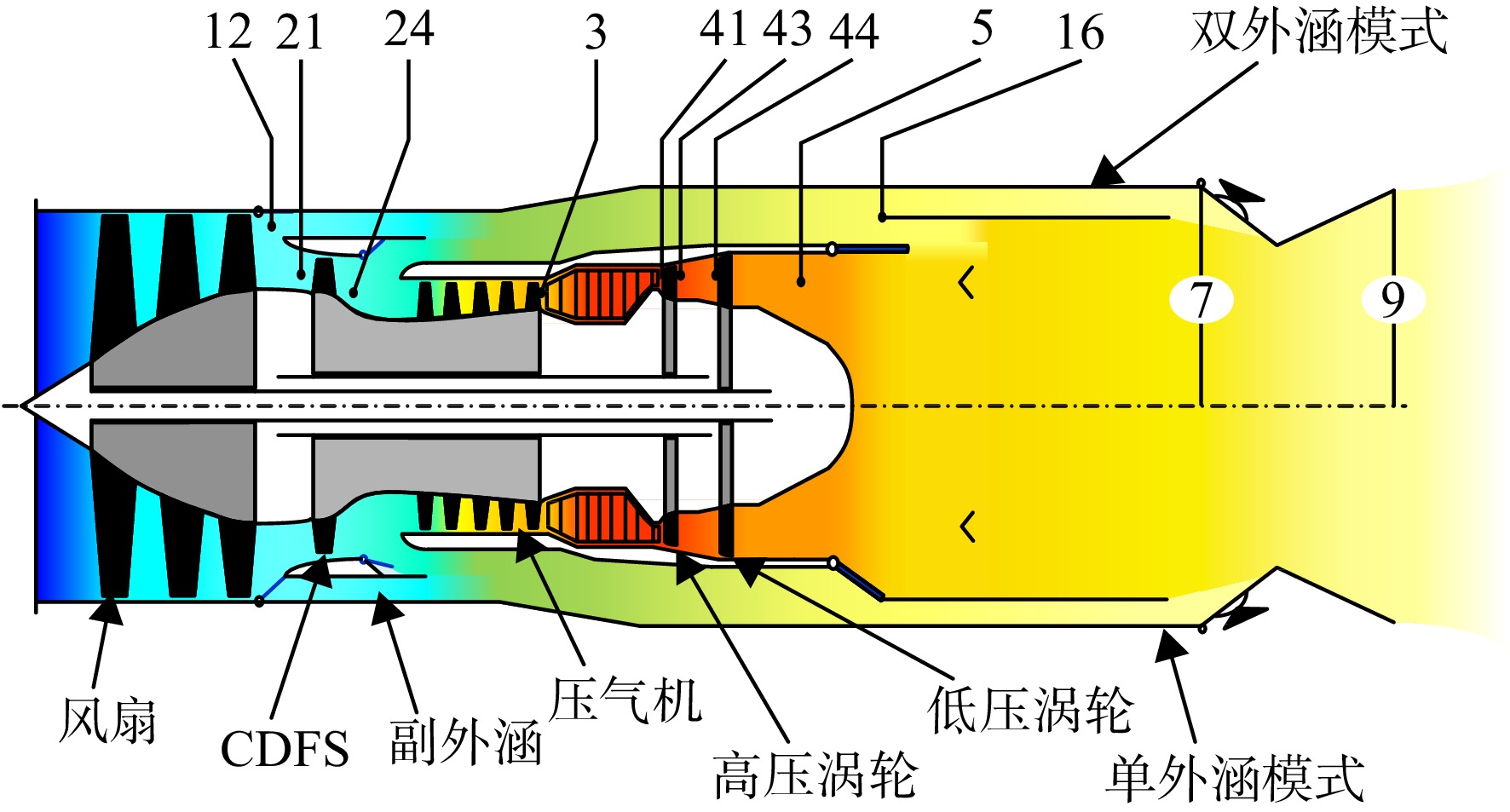
本文研究对象的气路部件图如图1所示。
与常见双转子混排涡扇发动机相比，在旋转部件结构上最大的区别就是将风扇分为两部分，且核心驱动风扇级（CDFS）布置在高压转子上，由高压涡轮带动，并因此产生双外涵道。如图1所示，21截面为风扇出口截面，24截面为CDFS出口截面，3截面为压气机出口截面，41截面为高压涡轮进口截面，43截面为高压涡轮出口截面，44截面为低压涡轮进口截面，5截面为低压涡轮出口截面，12截面为外涵进口截面，16截面为外涵出口截面，7截面为尾喷管进口截面，9截面为尾喷管出口截面。
本文研究对象主要有如下4个特点：
1） 模式选择活门（MSV）位于风扇出口，当处于双外涵模式时，MSV打开，否则MSV关闭；
2） CDFS由高压涡轮带转，位于高压轴；
3） 前可调涵道引射器（FVABI）主要用于平衡前部风扇出口气流与核心驱动风扇外涵出口气流的静压，可有效避免模式切换过程中副外涵的“倒流”问题，同时影响CDFS喘振裕度；
4） 后可调涵道引射器（RVABI）位于主混合室进口，其主要功能是调节主混合室静压平衡，影响外涵道流量。
VCE的可测输出传感器一般为低压转子转速、高压转子转速、风扇出口总温总压、核心驱动风扇级出口总温总压、压气机出口总温总压和低压涡轮出口总温总压传感器，即可测输出矩阵y=[nl, nh, T21, p21, T24, p24, T3, p3,T5, p5]，共计10个传感器，发动机的输入参数为环境参数，即高度、发动机进口马赫数、地面静温静压、主燃油流量、加力燃油量、各旋转部件导叶角度和尾喷管喉道面积。而燃烧室出口和高压涡轮出口截面由于温度过高，工作环境过于恶劣，在试车过程中，往往无法获取准确可靠的试车数据，而空气流量和推力在台架可测，而在飞行过程中并不进行测量，且在测量过程中分散度较大，且在用于稳态特性修模时，往往研究所不会提供较敏感的数据，因此，主要分析各特性修正参数变化对上述10个易于获取且可测传感器的影响，并寻找影响最大的特性参数进行求解，以达到模型修正的目的。
1.2 旋转部件特性修正系数选取
由于在发动机模型设计点确定后，各几何参数均无法改变，因此目前常见的修模主要是对特性图进行调整。为便于对特性图进行调整本文定义特性修正系数如式（1）：
hi=XiX∗ii=1,2,⋯,15 (1) 式中
Xi 为部件特性（如压比、效率和流量）修正后的值，X∗i 为部件特性的初值，下标i为部件特性参数的编号。为比较不同特性参数对模型可测输出的影响，分别将各特性参数减少相同的值，分析不同可测输出的变化情况。由图1可知，VCE共用5个旋转部件，分别是风扇、CDFS、压气机、高压涡轮和低压涡轮，每个旋转部件的特性参数共有3个分别是压比、效率和流量。为便于描述，将对特性参数和可测输出进行编号，所有特性修正系数的编号和符号如表1所示。
表 1 特性修正系数编号表Table 1. Identifiers of characteristic correction coefficients编号 物理意义 符号 1 风扇效率修正系数 h1 2 风扇流量修正系数 h2 3 风扇压比修正系数 h3 4 CDFS效率修正系数 h4 5 CDFS流量修正系数 h5 6 CDFS压比修正系数 h6 7 压气机效率修正系数 h7 8 压气机流量修正系数 h8 9 压气机压比修正系数 h9 10 高压涡轮效率修正系数 h10 11 高压涡轮流量修正系数 h11 12 高压涡轮压比修正系数 h12 13 低压涡轮效率修正系数 h13 14 低压涡轮流量修正系数 h14 15 低压涡轮压比修正系数 h15 分别对表1中的各特性修正系数减少1%～4%，在单涵模式和双涵模式下分别进行仿真，统计模型各可测输出的变化情况，选择去掉模型输出的变化较小的4个特性修正系数，即CDFS、压气机、高压涡轮和低压涡轮部件的压比修正系数。
以模型输出的平均变化值作为评价标准，输出平均变化值E定义为如式（2）所示：
Ei=11010∑j=1(y′i,j−yi,j)i=1,2,⋯,15 (2) 式中i为部件特性参数的编号，
yi,j 表示第i个特性修正系数发生变化前y中第j个参数的值，y′i,j 表示第i个特性修正系数发生变化后y中第j个参数的值。分别对表1中的各特性修正系数减少1%～4%，在单涵模式和双涵模式下分别进行仿真，统计模型各可测输出的变化情况仿真结果如图2所示。
如图2所示，单涵模式和双涵模式下，特性修正系数对输出的影响略有不同，从单涵模式看，5个旋转部件的压比特性对输出的影响最小，而从双涵模式看，除风扇压比外的4个压比特性对模型输出影响较小，但风扇压比对模型输出有一定影响。
使用NR迭代法对模型进行求解时必须保证方程具有唯一解，否则求出的解将无法表征发动机的状态。因此要对15个修正系数进行分析和筛选，获取主导的特性修正参数。
首先，综合考虑单涵模式和双涵模式下，特性变化对模型输出的影响，去掉CDFS、压气机、高压涡轮和低压涡轮部件的压比修正系数，这是因为4个参数无论是在单涵模式下还是双涵模式下，和其他特性修正系数相比，对模型的输出均影响较小。
然后去掉风扇压比修正系数。若不去除风扇压比修正系数，此时直接求解，仍会出现多解的情况。这是因为风扇出口截面只有2个传感器，无法对3个风扇的特性修正系数进行求解，因此风扇部件的3个特性修正系数必须至少去掉1个修正系数避免风扇部件的多解问题。从部件级模型稳定性的角度考虑，若将压比特性作为求取的特性，则压比特性的改变会导致流量和效率同时变化，加大了模型崩溃的概率，因此本文不选取风扇的压比特性作为主导特性修正参数之一。
此时共剩下10个特性修正系数，分别是5个旋转部件的效率和流量修正系数。但是为了确保唯一解，仍需要减少一个涡轮部件的特性修正系数。因为根据前后混合室静压守恒和尾喷管进出口的流量守恒，可以确定压缩部件的流量，从而确定整个发动机气路的流量，但是由于缺少涡轮间传感器的数据，特别是缺少涡轮间的压比传感器，在不知道共同工作点位置的情况下，无法确定涡轮部件流量和效率修正系数的值，因此涡轮部件的4个修正系数需要去掉1个，这样部件级模型才能得到唯一的涡轮压比，避免压比多解的情况。根据图2选择去掉对输出影响较小的低压涡轮效率系数。此时，选取的特性修正系数为h=[h1, h2, h4, h5, h7, h8, h10, h11, h14]。
2. 特性自修正双环策略设计
在文中第1节确定了修正系数矩阵h的基础上，本节将采用变阻尼系数NR迭代法对修正系数矩阵h进行求解，同时由于VCE模型本身旋转部件较多，且待求取的修正系数也较多，使用NR迭代法进行求取时极易出现模型崩溃的时候，且当多个试车点多个模型需要进行模型修正时，对模型自动修正算法的运行速度的提升也很有必要，因此本节主要介绍双环NR迭代法的结构，并提高算法稳定性和运行速度，并与常见的进行单点模型修正的NR迭代法进行比较。
2.1 耦合个体试车数据共同工作方程设计
常见的基于NR迭代的模型修正在针对单一试车点进行模型修正时，是一种双层的结构，外层NR迭代用来计算对特性图的修正系数并对特性图进行修正，而内层NR迭代则用于求解部件级模型的转速和压比，用于部件级模型的气路计算，其结构图如图3所示。
如图3所示，由于迭代环节较多，双层NR迭代在多试车点多模型修正时运行耗时较多，且由于迭代环节较多，易发生模型崩溃或外层NR迭代崩溃的问题，本文对上述两个方面进行改善。首先耗时主要是两个方面：①内层NR迭代的耗时，主要是由于模型本身求解待求解参数（转速和压比）导致的耗时，本文通过逆流路法进行改善；②外层NR迭代为了更新特性图，每次都需要对修正系数进行扰动，此时每次扰动都需要运行1次内层的模型，需要消耗大量仿真时间，本文通过将其改为单层NR迭代进行改善。
而算法运行的稳定性问题主要有以下3个原因：①模型自身利用NR迭代时，由于固定步长的NR迭代算法容易将模型的待求解参数的范围更新至0～1范围之外，导致模型运行崩溃；②转子部件的压比在求解过程中超出了特性图的覆盖范围，导致模型崩溃；③当前特性修正系数不合理，导致内层NR迭代崩溃。上述3个问题本文通过变阻尼系数NR迭代法对模型每次迭代后待求解的值进行优化，以提高模型稳定性。
单层NR迭代法和双层NR迭代的主要差别在于将原模型的待求解参数利用试车数据计算而不参与迭代，将特性修正系数和无法利用试车数据求解的模型待求解参数作为新的模型输入参数，而将模型输出与试车数据的误差和原模型的平衡方程作为新的方程组，利用NR迭代法进行求解，结构图如图4所示。
如图4所示，h是第i个试车点的特性修正系数矩阵。由于压缩部件出口压力传感器和涡轮出口压力传感器都是可测传感器,因此涡轮部件的总落压比是已知的，因此只需将其中一个部件的压比作为模型的待求解值，即可表示另一个涡轮部件的压比，而原模型中转速和其他压比均可根据试车数据计算得到。
因此针对个体试车数据进行耦合后，模型使用的平衡方程共10个，分别是：
1） 风扇出口流量
W2 与CDFS进口流量W23 以及外涵道进口流量W12 平衡（W12+W23）/（W12+W23）W2−1=0W2−1=0 (3) 2） 燃烧室出口流量
W4 与高压涡轮进口流量W41 平衡W41/W41W4−1=0W4−1=0 (4) 3） 高压涡轮出口流量
W43 与低压涡轮进口流量W44 平衡W44/W44W43−1=0W43−1=0 (5) 4） 尾喷管进口流量
W7 与出口流量W9 平衡W9/W9W7−1=0W7−1=0 (6) 5） 外涵道出口静压
ps16 与内涵出口静压ps5 平衡ps16/ps16ps5−1=0ps5−1=0 (7) 6） 高压转子功率平衡方程
（Pht−Pex）ηh/（Pht−Pex）×ηh（Pc+Pcd）−1=0（Pc+Pcd）−1=0 (8) 式中
Pht 为高压涡轮输出功率，Pc 为压气机消耗功率，Pcd 为CDFS消耗功率，Pex 为附件提取功率，ηh 为高压轴机械效率。7） 低压转子功率平衡方程
Pltηl/PltηlPfPf−1=0 (9) 式中
Plt 为低压涡轮输出功率，Pf 为风扇消耗功率，ηl 为低压轴机械效率。8） 试车数据的风扇出口温度T21,r和模型风扇出口总温T21,m相等方程
T21,m=T21,r (10) 9） 试车数据的CDFS出口温度T24,r和模型的CDFS出口温度T24,m输出相等方程
T24,m=T24,r (11) 10） 试车数据的压气机出口温度T3,r和模型输出T3,m相等方程
T3,m=T3,r (12) 通过将式（3）～式（12）共计10个方程直接放入模型中，可以利用NR迭代法求解主导特性修正系数矩阵h中的元素及低压涡轮的压比。
同时通过将试车数据耦合进入共同工作方程的方法，可以针对同型号不同发动机的个体差异进行针对性修正，提高了身份证动态模型的输出精度。
2.2 多点修正的双环策略
由于基于单层NR迭代法的模型自动修正算法只能针对单个试车点进行修正，而工程应用中，往往需要根据多个试车点对特性图整体进行修正，本文采取多工作状态一致修正方法将求取的特性修正系数扩展至全特性图，其结构图如图5所示。
图 5 基于NR迭代法的多点模型自动修正方法Figure 5. Automatic multi-point correction method based on NR method多工作状态一致修正方法主要根据部件进口相似换算转速从高到低的顺序，依次对特性图进行修正，本文以压气机为例，阐述多工作状态一致修正的思想，压气机局部特性如图6所示。
如图6所示，试车点A、B和C所在特性线转速依次降低，本文根据部件进口相似换算转速“由高到低”的顺序进行修正。首先需要对点A进行修正，由于点A是最高转速试车点，因此为了不影响设计点，在修正点A时，对部件特性图上的所有转速不高于A点的特性线进行缩放，这种方法的好处在于如果发动机部件特性与真实发动机的实际特性差距较大时，对于高转速点的整体缩放可以减小较低转速的误差，为之后求取如点B修正系数的求取提供便利，否则由于初始模型和试车数据差距较大，极易导致修正低转速点时使得模型崩溃。点A修正完毕后，对换算转速仅低于点A的点B进行修正。为了保证在修正点B时不会影响到点A，需要固定点A所在的特性线L1及更高转速线不变，缩放L2及其以下的所有特性线，再者，修正换算转速仅小于点A和点B的点C，方法同修正点B时类似，固定转速高于C的特性线，对转速低于L3及L3进行缩放，特性线L1、L2和L3在缩放后如
L′1 、L′2 和L′3 所示。通过对共同工作方程的设计和多工作点的双环修模策略的设计，仅需输入发动机输入参数及试车数据的条件下，即可以自动对特性图进行修正，进而自动修正身份证动态模型的输出精度，实现自动模型修正的目的。
3. 增强型身份证动态模型快速计算方法
文中第2节已经设计了VCE的身份证模型自动修正双环策略，但由于部件级模型的复杂性和特殊性，所建立的模型自动修正策略的实时性和稳定性需要进一步提升，以加强工程应用的成功性。
本节通过逆流路扰动法，缩短模型自动修正算法的耗时，通过NR迭代阻尼系数的自调整和特性图外插保护逻辑的设计提高了算法的稳定性，设计了增强型身份证模型自动修正双环策略，并与文中第2节的算法进行比较。
3.1 基于逆流路扰动的快速计算方法
由于双层NR迭代每次外层迭代扰动求导数时，均需完整运行1次内层的部件级模型，因此耗时较多，且在工程实际中，往往1个型号的发动机需要进行成百上千次的模型修正，因此尽可能提高算法的运行速度是工程上的迫切需求之一。
先对部件级模型各主要部件的耗时进行统计和分析。在2.10 GHz处理器的计算机上进行仿真，连续运行部件级模型20万次，各主要部件耗时如表2所示。
表 2 VCE模型各主要部件耗时Table 2. Time consumption of main components of VCE部件 耗时/ms 占比/% 部件 耗时/ms 占比/% 进气道 19 0.2 高压涡轮 1417 14.83 风扇 1760 18.43 低压涡轮 1623 16.99 CDFS 1762 18.45 外涵道 184 1.93 压气机 2164 22.65 尾喷管 581 6.08 燃烧室 42 0.44 为进一步发现耗时的主要部件，绘制耗时占比图，主要用于突出显示旋转部件的耗时占比，如图7所示。
如图7所示，5个旋转部件的耗时占总耗时的约91.35%，而由于基于单层NR迭代法的模型待求解量有10个参数，常见的顺气路扰动需要分别对10个参数进行扰动，此时1次完整的迭代需要调用11次气路计算，因此每个转子部件均需调用11次，而大量的气路计算仅是用来对平衡方程进行求导，而在求导过程中，各待求解参数并不是对全部气路过程都会造成影响，各待求解参数在气路计算中参与工作的位置及对单次气路扰动影响的区域如图8所示。
图 8 待求解参数在气路计算中参与工作位置图Figure 8. Working position of the parameters to be solved in the gas path calculation如图8所示，由于在求导过程中，扰动在气路后方的参数一般不会对前侧部件造成影响，因此，采用逆流路扰动法，从后向前扰动各待求解参数，此时对旋转部件的扰动次数分别如图8所示，相比常规气路计算，有效减少了旋转部件的调用次数。与常规的顺流路扰动不同，采用逆流路扰动可以减少前侧部件的调用次数，有效减少了旋转部件在求导过程中参与运算的次数。且用于在扰动待求参数的过程中，尾喷管仅需提供出口流量，而尾喷管部件的耗时主要在求取马赫数和静压从而判断尾喷管的状态方面，而由于对待求参数的扰动量仅有0.000 5，基本不会对尾喷管的状态判断构成影响，因此1次迭代仅对尾喷管的状态进行1次判断，从而简化求导过程中的尾喷管模型，节省仿真时间。
3.2 NR迭代阻尼系数自调整
针对文中第2.1节中模型稳定性的问题，使用了变阻尼系数NR迭代法提高模型稳定性。常见的NR迭代法的公式如式（13）所示：
xn+1=xn−f（xn）f′（xn） (13) 式中xn为第n时刻发动机部件级模型中的待求解参数，f （xn）为发动机非线性函数，f ′（xn）为发动机非线性函数的导函数。由于发动机的待求解参数如转速和压比可取值的范围较小，若n时刻f （xn）/f ′（xn）单步值过大，则n+1时刻发动机模型的待求解参数易超出合理范围，容易导致特性图外插等问题的出现，导致模型崩溃，因此在实际应用过程中，往往会设置1个常数阻尼系数，如式（14）所示
xn+1=xn−λf（xn）f′（xn） (14) 式中λ为一个常数，称为NR迭代阻尼系数。阻尼系数的设定往往需要手动调整。当阻尼系数设定较大时，容易导致模型崩溃或使xn在真值附近振动，无法收敛；而当阻尼系数设定较小时，会影响模型的收敛速度，极大影响发动机模型的运行速度。因此为避免模型的崩溃，
λ 的选取应最好与的f （xn）/f ′（xn）值有关，在f （xn）/f ′（xn）较大时，可以有效减小xn单步的调整量，保持模型的稳定性；而在f （xn）/f ′（xn）较小时，不影响模型的收敛速度，也不会导致xn在真值附近波动。因此将阻尼系数λ 设定为可以根据f （xn）/f ′（xn）的值自适应变化的变量，其值的选取定义为式（15）：{λ=0.01f（xn）f′（xn）,f（xn）f′（xn）>0.05λ=0.2,f（xn）f′（xn）⩽ (15) 当λ如式（15）所示自适应变化时，单步对xn的调整量如图9所示。
图 9 NR迭代阻尼系数自调整法调整量变化图Figure 9. Change of self adjustment of NR method damping coefficient图9中虚线指的是采用如式（14）时单步调整量的变化，λ指的是数值固定的阻尼系数，λ'指的是本文设计的变阻尼系数。如图9的点划线可知，采用阻尼系数自调整法，xn的单步调整量不会大于0.01，因此不会使得模型的待求解量轻易超出合理范围，保证了模型的稳定性。而如式（14）采用常值
\lambda 时，会使得f （xn）/f ′（xn）过大时，导致单步调整量过大，使得模型崩溃。且在初猜值不合理时，由于缩小了单步的调整量的大小，因此某些使用NR迭代法无法收敛的情况下，使用变阻尼系数的NR迭代法可以收敛，扩大了NR迭代搜索解的范围，提高了模型稳定性。3.3 特性图外插保护逻辑
为进一步提高模型的稳定性，对特性图的外插逻辑进行优化。在模型迭代收敛的过程中，最容易出现的崩溃原因之一就是部件特性图外插后偏离正常值，导致模型无法继续迭代。此时，往往并不代表模型不存在解，而只是因为不合理的特性图外插逻辑导致共同工作点无法回到特性图所覆盖的范围内。常见的特性图插值逻辑如式（16）～ 式（17）所示。
设函数u=f （v），v
\in [a, b], a, b\in R，R为实数集，设待插值变量u2的横坐标为v2，v2\in （v0, v1）\subset [a, b]，满足：u_{0}=f （v_{0}） \quad\quad u_{1}=f （v_{1}） (16) 则通过线性插值得到的u2为
{u_2} = {u_0} + \frac{{{u_1} - {u_0}}}{{{v_1} - {v_0}}} （{v_2} - {v_0}） (17) 式（17）表示的是v2在[a, b]范围内时的插值方法，当应用到特性图上时，即压比在特性图覆盖的范围内时，采用式（17）的插值逻辑，当压比超出特性图的覆盖范围，此时常见的线性插值逻辑如式（18）所示。
设特性线的数据点共有k个，从左至右分别为v1,···, vk，其在特性线上的纵坐标分别为u1,···, uk，则当v>vk或v<v1时，常见线性插值为
\left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{c}} {u = {u_k} + \dfrac{{{u_k} - {u_{k - 1}}}}{{{v_k} - {v_{k - 1}}}} （{v_k} - v） },&{v > {v_k}} \end{array}} \\ {\begin{array}{*{20}{c}} {u = {u_1} + \dfrac{{{u_2} - {u_1}}}{{{v_2} - {v_1}}} （{v_1} - v） },&\;\;\;{v < {v_1}} \end{array}} \end{array}} \right. (18) 由式（18）可知，当压比超出特性图的范围时，此时常见的线性插值逻辑会按照特性线边缘的导数向外扩展，而特性线在两侧边缘的导数的绝对值往往较大，因此在迭代过程中，当压比超限时，往往算法无法收敛，因此改变特性图超限时的插值逻辑，改变后插值逻辑如式（19）所示：
\left\{ {\begin{array}{*{20}{c}} {u = {u_k}}&{v > {v_k}} \\ {u = {u_1}}&{v < {v_1}} \end{array}} \right. (19) 此时，当压比超出特性图的范围时，流量和效率不会继续插值，而是会等于特性线两端的端点值，此时发动机模型的气路计算不会轻易崩溃，可以继续收敛计算直至得到合适的解，进一步提高了模型的稳定性。
4. 仿真验证
4.1 稳态精度仿真验证
针对该型VCE模型的某组试车值，采用增强型身份证模型自动修正双环策略，对部件级模型进行模型修正，本文采取稳态误差对稳态精度进行考察，修正后各试车值的稳态误差定义为
{e_{{\text{j}}}} = \frac{{{y_{\text{b}}} - \widehat y}}{{{y_{\text{b}}}}} \times 100{\text{%}} (20) 式中yb是试车值，
\widehat{\mathit{y}} 是修正后部件级模型的输出。分别采用文中第2节中介绍的不同收敛精度的双层和单层NR迭代法对部件级模型进行修正，修正后各试车值稳态精度如表3及表4所示。
表 3 基于双层NR迭代法模型修正后输出平均误差表Table 3. Average output error after model correction based on double-loop NR method% 发动机模式 外层收敛精度 nl nh T21 p21 T24 p24 T3 p3 T5 p5 单涵 0.1 0.010 0.036 0.033 0.012 0.020 0.049 0.031 0.082 0.117 0.096 0.5 0.048 0.178 0.161 0.061 0.101 0.241 0.156 0.400 0.569 0.472 1.0 0.094 0.348 0.306 0.116 0.182 0.475 0.279 0.787 1.112 0.928 2.0 0.177 0.679 0.602 0.235 0.360 0.924 0.551 1.533 2.152 1.811 双涵 0.1 0.048 0.035 0.005 0.033 0.001 0.065 0.014 0.092 0.140 0.089 0.5 0.214 0.170 0.030 0.130 0.012 0.285 0.086 0.404 0.776 0.468 1.0 0.418 0.358 0.062 0.283 0.023 0.625 0.173 0.878 1.475 0.929 2.0 0.971 0.724 0.124 0.616 0.029 1.330 0.323 1.822 2.608 1.749 表 4 基于单层NR迭代法模型修正后输出平均误差表Table 4. Average output error after model correction based on single-loop NR method% 发动机模式 nl nh T21 p21 T24 p24 T3 p3 T5 p5 单涵 0 0 0.001 0 0.001 0 0.003 0 0.051 0 双涵 0 0 0.008 0 0.011 0 0.020 0 0.088 0 由表3和表4可知，使用基于双层NR迭代法模型双环自动修正策略修正后的模型，受NR迭代的外层收敛精度影响，外层收敛精度越低，误差越大，而两种方法中T5的误差相比于其他传感器较大。这主要是因为T5的精度是依靠功率守恒间接保证的，因此误差要略大于收敛精度。
因此当使用双层NR迭代法时，若需要较高的模型输出精度，则需要较低的外层收敛精度，则耗时会进一步提升，而采用本文的单层NR迭代法时，不仅在精度上不输于双层法，而且在耗时上会远少于双层法。
4.2 模型特性仿真分析
通过采取多工作状态一致修正方法，本文成功对全特性图进行修正，修正后的特性图应该基本保持修正前特性图的变化趋势和部分特征。为验证修正后特性图的合理性，对修正前后不同转速N下的特性图进行比较，如图10所示。
图 10 修正前后压缩部件部分特性图比较图Figure 10. Comparison of partial characteristic maps of compressor before and after correction图10中，虚线为修正前特性图（用ori表示），实线为修正后特性图，图中图例为每一根等转速线所对应的转速。由图10可知，修正前后的特性图的变化趋势基本没有变化，且各特性线之间没有交叉，避免了模型出现多解的情况，且基本确保了模型的输出曲线光滑。
为验证多点同时修正的有效性，由于篇幅有限，以风扇部件部分特性线的修正系数为例进行计算分析，如表5所示。
表 5 风扇部件部分特性修正系数Table 5. Partial characteristic correction coefficients of fan components转速 流量修正系数 效率修正系数 0.70 0.947 0.951 0.80 0.973 0.969 0.90 0.981 0.980 0.95 0.981 0.980 1.00 0.981 0.980 由表5可知，各特性线均进行了修正，且在试车转速范围内的特性线的修正系数均不相同，而不在试车转速范围内的特性线也根据超限逻辑进行了合理的缩放，以保证特性图的合理性。
4.3 共同工作点仿真分析
为验证所修正后模型在大范围转速内的效果，验证在试车点共同工作点是否合理，以单涵模式为例，考察单涵模式特性图修正后共同工作点的位置，如图11所示。
图 11 单涵模式特性图修正后共同工作点分布图Figure 11. Distribution of cooperating points after correction of characteristic maps of single culvert mode如图11所示，特性图（用ori表示），实线为修正后特性图，图中图例为每一根等转速线所对应的转速。在单涵模式下，修正后的身份证动态模型的共同工作点仍能在大范围转速内保持较好的位置，既保持了一定的喘振裕度又能在较高效率位置运行，这表明修正后的特性图可以使得发动机模型工作在性能较好的位置，可以较好模拟实际发动机的工作状况。
在和试车值相同的高度马赫数下，使燃油斜坡下降，在双涵模式特性图修正前后动态模型的输出如图12所示。
图 12 双涵模式特性图修正后共同工作点分布图Figure 12. Distribution of cooperating points after correction of characteristic maps of double culvert mode如图12所示，特性图（用ori表示），实线为修正后特性图，图中图例为每一根等转速线所对应的转速。在双涵模式下，修正后的身份证动态模型的共同工作点仍能在大范围转速内保持较好的位置，这表明修正后的特性图可以使得发动机模型工作在性能较好的位置，对发动机的实际工作状态有一定的参考价值。
图11和图12说明，在较大转速范围内，修正后的特性图基本保持发动机的共同工作点在性能较好的位置，表明修正后的模型可以对发动机实际工作点提供参考，有积极的工程意义。
4.4 模型计算耗时分析验证
验证基于逆流路法和单层NR迭代结构相比于双层NR迭代结构在运行速度上的优势，本节分别从以下两个方面进行仿真验证：①通过比较使用身份证模型自动修正双环策略和增强型身份证模型自动修正双环策略的耗时，验证增强型设计对算法运行速度的提升；②通过比较增强型与常规自动修正双环策略与常见双层NR迭代法模型修正法的耗时，验证本文所设计的身份证模型自动修正算法相比于常见双层NR迭代法在计算耗时上的提升。
首先，对常规双层NR迭代法不同外层收敛精度对运算耗时的影响进行仿真，如图13所示。
图 13 常规双层NR不同外层收敛精度迭代耗时比较图Figure 13. Time-consuming comparison of conventional double-loop NR method with different outer convergence accuracy如图13所示，可以较为明显地发现，随着外层NR迭代的收敛精度的增大，耗时明显减少，这是因为外层所需的迭代次数减少，所以较大减少了所需运行内层模型的时间，由此也可以证明，常规双层NR迭代法需要在精度和耗时之间根据实际需要进行权衡调整。
其次，分别在单、双涵模式下对身份证模型自动修正双环策略、增强型身份证模型自动修正双环策略进行仿真验证，分析各方法的耗时情况，如表6所示。
表 6 增强型与常规自动修正双环策略耗时比较表Table 6. Comparison of time consumption between enhanced and conventional automatic correction double-loop strategies修正方法 发动机模式 外层收敛精度 耗时/s 身份证模型自动
修正双环策略单涵 0.001 0.08 双涵 0.001 0.11 增强型身份证模型
自动修正双环策略单涵 0.001 0.05 双涵 0.001 0.07 如表6所示，增强型双环策略在单涵和双涵模式下相对于未进行增强的模型，其耗时节省分别约37.5%和36.4%，这表明本文所设计的增强型双环策略对算法的运行速度有较大的提升。
为了进一步分析增强型双环策略和常规双层NR迭代法的运行耗时比较，选取常规双层NR迭代外层收敛精度为0.001，不同模式下，3种耗时如图14所示。
如图14所示，采用双环单层自动修正策略的耗时和外层收敛精度为0.001的常规双层NR迭代法相比，节省耗时均在99%以上。这主要是由于双层NR迭代时，每次外层迭代扰动求导时，均需运行1次内层的模型，导致大量耗时。
如图13和图14可知，在4种不同的外层收敛精度下，增强型身份证模型自动修正双环策略相对于常规双层NR迭代策略节省耗时均超过98.6%，因此使用增强型身份证模型自动修正双环策略可以同时保证修正后的模型有较高的输出精度和较低的算法耗时。
5. 结 论
1） 通过对VCE各旋转部件的特性修正系数进行分析，选取了利用可测传感器组合可以求解出唯一解的主导特性修正系数组合。
2） 提出了增强型身份证模型特性自动修正双环策略，包含针对双环单层模型自动修正策略的设计、耦合个体试车数据以建立新平衡方程、提出逆流路扰动法提高模型运行速率、采用NR迭代阻尼系数自调整和特性图保护逻辑有效改善模型稳定性，使所提出的增强型模型自动修正算法可依据工程需要快速自动修正模型，为其他相关研究提供模型参考。
3） 所设计的模型自动修正方法使修正后模型的输出误差小于0.1%，和常规双层NR迭代法的0.14%相比，最大误差减小了约28.6%，在2.10 GHz处理器的计算机上单涵模式耗时约0.08 s，双涵模式耗时约0.11 s，方法耗时比未增强的身份证模型自动修正策略节省耗时36.4%以上，比常规双层NR迭代法减少98.6%以上。
-
图 5 基于NR迭代法的多点模型自动修正方法
Figure 5. Automatic multi-point correction method based on NR method
图 8 待求解参数在气路计算中参与工作位置图
Figure 8. Working position of the parameters to be solved in the gas path calculation
图 9 NR迭代阻尼系数自调整法调整量变化图
Figure 9. Change of self adjustment of NR method damping coefficient
图 10 修正前后压缩部件部分特性图比较图
Figure 10. Comparison of partial characteristic maps of compressor before and after correction
图 11 单涵模式特性图修正后共同工作点分布图
Figure 11. Distribution of cooperating points after correction of characteristic maps of single culvert mode
图 12 双涵模式特性图修正后共同工作点分布图
Figure 12. Distribution of cooperating points after correction of characteristic maps of double culvert mode
图 13 常规双层NR不同外层收敛精度迭代耗时比较图
Figure 13. Time-consuming comparison of conventional double-loop NR method with different outer convergence accuracy
表 1 特性修正系数编号表
Table 1. Identifiers of characteristic correction coefficients
编号 物理意义 符号 1 风扇效率修正系数 h1 2 风扇流量修正系数 h2 3 风扇压比修正系数 h3 4 CDFS效率修正系数 h4 5 CDFS流量修正系数 h5 6 CDFS压比修正系数 h6 7 压气机效率修正系数 h7 8 压气机流量修正系数 h8 9 压气机压比修正系数 h9 10 高压涡轮效率修正系数 h10 11 高压涡轮流量修正系数 h11 12 高压涡轮压比修正系数 h12 13 低压涡轮效率修正系数 h13 14 低压涡轮流量修正系数 h14 15 低压涡轮压比修正系数 h15 
下载: 导出CSV
表 2 VCE模型各主要部件耗时
Table 2. Time consumption of main components of VCE
部件 耗时/ms 占比/% 部件 耗时/ms 占比/% 进气道 19 0.2 高压涡轮 1417 14.83 风扇 1760 18.43 低压涡轮 1623 16.99 CDFS 1762 18.45 外涵道 184 1.93 压气机 2164 22.65 尾喷管 581 6.08 燃烧室 42 0.44
下载: 导出CSV
表 3 基于双层NR迭代法模型修正后输出平均误差表
Table 3. Average output error after model correction based on double-loop NR method
% 发动机模式 外层收敛精度 nl nh T21 p21 T24 p24 T3 p3 T5 p5 单涵 0.1 0.010 0.036 0.033 0.012 0.020 0.049 0.031 0.082 0.117 0.096 0.5 0.048 0.178 0.161 0.061 0.101 0.241 0.156 0.400 0.569 0.472 1.0 0.094 0.348 0.306 0.116 0.182 0.475 0.279 0.787 1.112 0.928 2.0 0.177 0.679 0.602 0.235 0.360 0.924 0.551 1.533 2.152 1.811 双涵 0.1 0.048 0.035 0.005 0.033 0.001 0.065 0.014 0.092 0.140 0.089 0.5 0.214 0.170 0.030 0.130 0.012 0.285 0.086 0.404 0.776 0.468 1.0 0.418 0.358 0.062 0.283 0.023 0.625 0.173 0.878 1.475 0.929 2.0 0.971 0.724 0.124 0.616 0.029 1.330 0.323 1.822 2.608 1.749
下载: 导出CSV
表 4 基于单层NR迭代法模型修正后输出平均误差表
Table 4. Average output error after model correction based on single-loop NR method
% 发动机模式 nl nh T21 p21 T24 p24 T3 p3 T5 p5 单涵 0 0 0.001 0 0.001 0 0.003 0 0.051 0 双涵 0 0 0.008 0 0.011 0 0.020 0 0.088 0
下载: 导出CSV
表 5 风扇部件部分特性修正系数
Table 5. Partial characteristic correction coefficients of fan components
转速 流量修正系数 效率修正系数 0.70 0.947 0.951 0.80 0.973 0.969 0.90 0.981 0.980 0.95 0.981 0.980 1.00 0.981 0.980
下载: 导出CSV
表 6 增强型与常规自动修正双环策略耗时比较表
Table 6. Comparison of time consumption between enhanced and conventional automatic correction double-loop strategies
修正方法 发动机模式 外层收敛精度 耗时/s 身份证模型自动
修正双环策略单涵 0.001 0.08 双涵 0.001 0.11 增强型身份证模型
自动修正双环策略单涵 0.001 0.05 双涵 0.001 0.07
下载: 导出CSV
-
[1] 唐海龙. 面向对象的航空发动机性能仿真系统及其应用[D]. 北京: 北京航空航天大学,2000. TANG Hailong. Object-oriented aero-engine performance simulation system and its application[D]. Beijing: Beihang University,2000. (in ChineseTANG Hailong. Object-oriented aero-engine performance simulation system and its application[D]. Beijing: Beihang University, 2000. (in Chinese) [2] 周红,王占学,刘增文,等. 双外涵变循环发动机可变几何特性研究[J]. 航空学报,2014,35(8): 2126-2135. ZHOU Hong,WANG Zhanxue,LIU Zengwen,et al. Variable geometry characteristics research of double bypass variable cycle engine[J]. Acta Aeronautica et Astronautica Sinica,2014,35(8): 2126-2135. (in ChineseZHOU Hong, WANG Zhanxue, LIU Zengwen, et al. Variable geometry characteristics research of double bypass variable cycle engine[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(8): 2126-2135. (in Chinese) [3] DU Xian,GUO Yingqing,SUN Hao. An adaptive model predictive controller for turbofan engines[J]. American Journal of Engineering Research,2015,4(12): 170-176. [4] 郑铁军,王曦,罗秀芹,等. 建立航空发动机状态空间模型的修正方法[J]. 推进技术,2005,26(1): 46-49. ZHENG Tiejun,WANG Xi,LUO Xiuqin,et al. Modified method of establishing the state space model of aeroengine[J]. Journal of Propulsion Technology,2005,26(1): 46-49. (in ChineseZHENG Tiejun, WANG Xi, LUO Xiuqin, et al. Modified method of establishing the state space model of aeroengine[J]. Journal of Propulsion Technology, 2005, 26(1): 46-49. (in Chinese) [5] KURZKE J. How to get component maps for aircraft gas turbine performance calculations[R]. ASME Paper 96-GT-164,1996. [6] 贾琳渊,程荣辉,张志舒,等. 研发阶段涡扇发动机模型自适应方法[J]. 推进技术,2020,41(9): 1935-1945. JIA Linyuan,CHENG Ronghui,ZHANG Zhishu,et al. Adaptive modelling for turbofan engine in development stage[J]. Journal of Propulsion Technology,2020,41(9): 1935-1945. (in ChineseJIA Linyuan, CHENG Ronghui, ZHANG Zhishu, et al. Adaptive modelling for turbofan engine in development stage[J]. Journal of Propulsion Technology, 2020, 41(9): 1935-1945. (in Chinese) [7] 周文祥. 航空发动机及控制系统建模与面向对象的仿真研究[D]. 南京: 南京航空航天大学,2006. ZHOU Wenxiang. Research on object-oriented modeling and simulation for aeroengine and control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2006. (in ChineseZHOU Wenxiang. Research on object-oriented modeling and simulation for aeroengine and control system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006. (in Chinese) [8] 姚华. 航空发动机全权限数字电子控制系统[M]. 北京: 航空工业出版社,2014: 22-32. [9] 俞明帅. 航空发动机模型组态与修正技术研究[D]. 南京: 南京航空航天大学,2012. YU Mingshuai. Research on configuration and correction technology for aero-engines modeling[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2012. (in ChineseYU Mingshuai. Research on configuration and correction technology for aero-engines modeling[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2012. (in Chinese) [10] 钟文城,汪勇,宋劼,等. 一种面向航空发动机数学模型的新型修正方法[J]. 航空动力学报, 2023, 38(11):2776-2784. ZHONG Wencheng,WANG Yong,SONG Jie,et al. A new correction method for aero-engine mathematical model[J]. Journal of Aerospace Power, 2023, 38(11):2776-2784.ZHONG Wencheng, WANG Yong, SONG Jie, et al. A new correction method for aero-engine mathematical model[J]. Journal of Aerospace Power, 2023, 38（11）: 2776-2784. [11] 郑斐华. 基于系统辨识的航空发动机建模研究[D]. 北京: 中国科学院大学,2018. ZHENG Feihua. Aeroengine modeling research based on system identification[D]. Beijing: Chinese Academy of Sciences,2018. (in ChineseZHENG Feihua. Aeroengine modeling research based on system identification[D]. Beijing: Chinese Academy of Sciences, 2018. (in Chinese) [12] 潘鹏飞. 高精度航空发动机机载自适应实时模型研究[D]. 南京: 南京航空航天大学,2014. PAN Pengfei. Research on high-accuracy on-board real-time adaptive model of aero-engine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2014. (in ChinesePAN Pengfei. Research on high-accuracy on-board real-time adaptive model of aero-engine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2014. (in Chinese) [13] LI Y G,ABDUL GHAFIR M F,WANG L,et al. Nonlinear multiple points gas turbine off-design performance adaptation using a genetic algorithm[J]. Journal of Engineering for Gas Turbines and Power,2011,133(7): 42-50. [14] TSOUTSANIS E,MESKIN N,BENAMMAR M,et al. A component map tuning method for performance prediction and diagnostics of gas turbine compressors[J]. Applied Energy,2014,135: 572-585. [15] TSOUTSANIS E,MESKIN N,BENAMMAR M,et al. Transient gas turbine performance diagnostics through nonlinear adaptation of compressor and turbine maps[J]. Journal of Engineering for Gas Turbines and Power,2015,137(9): 091201. [16] 王军,隋岩峰. 整机条件下涡扇发动机部件特征参数辨识[J]. 航空动力学报,2013,28(3): 666-672. WANG Jun,SUI Yanfeng. Identification of component characteristic parameter for whole turbofan engine[J]. Journal of Aerospace Power,2013,28(3): 666-672. (in ChineseWANG Jun, SUI Yanfeng. Identification of component characteristic parameter for whole turbofan engine[J]. Journal of Aerospace Power, 2013, 28(3): 666-672. (in Chinese) [17] VISSER W P J,KOGENHOP O,OOSTVEEN M. A generic approach for gas turbine adaptive modeling[J]. Journal of Engineering for Gas Turbines and Power,2006,128(1): 13-19. [18] 潘阳. 涡轴发动机控制系统传感器故障诊断与容错控制[D]. 南京: 南京航空航天大学,2016. PAN Yang. Research on turbo-shaft engine control system sensor fault diagnosis and fault tolerant control[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2016. (in ChinesePAN Yang. Research on turbo-shaft engine control system sensor fault diagnosis and fault tolerant control[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2016. (in Chinese) [19] 陈玉春,徐思远,屠秋野,等. 求解航空发动机非线性方程组的变步长牛顿法[J]. 航空计算技术,2009,39(1): 39-41,44. CHEN Yuchun,XU Siyuan,TU Qiuye,et al. Variable step Newton method for solving the nonlinear equations of aero turbine engines[J]. Aeronautical Computing Technique,2009,39(1): 39-41,44. (in ChineseCHEN Yuchun, XU Siyuan, TU Qiuye, et al. Variable step Newton method for solving the nonlinear equations of aero turbine engines[J]. Aeronautical Computing Technique, 2009, 39(1): 39-41, 44. (in Chinese) [20] 段守付,樊思齐,卢燕. 航空发动机自适应建模技术研究[J]. 航空动力学报,1999,14(4): 440-442,457. DUAN Shoufu,FAN Siqi,LU Yan. Adaptive modelling technique for aeroengine[J]. Journal of Aerospace Power,1999,14(4): 440-442,457. (in ChineseDUAN Shoufu, FAN Siqi, LU Yan. Adaptive modelling technique for aeroengine[J]. Journal of Aerospace Power, 1999, 14(4): 440-442, 457. (in Chinese) [21] LU Feng,HUANG Jinquan,JI Chunsheng,et al. Gas path on-line fault diagnostics using a nonlinear integrated model for gas turbine engines[J]. International Journal of Turbo & Jet-Engines,2014,31(3): 261-275. [22] 陆军,郭迎清,张书刚. 基于改进混合卡尔曼滤波器的航空发动机机载自适应模型[J]. 航空动力学报,2011,26(11): 2593-2600. LU Jun,GUO Yingqing,ZHANG Shugang. Aeroengine on-board adaptive model based on improved hybrid Kalman filter[J]. Journal of Aerospace Power,2011,26(11): 2593-2600. (in ChineseLU Jun, GUO Yingqing, ZHANG Shugang. Aeroengine on-board adaptive model based on improved hybrid Kalman filter[J]. Journal of Aerospace Power, 2011, 26(11): 2593-2600. (in Chinese) [23] LI Y G,PILIDIS P,NEWBY M A. An adaptation approach for gas turbine design-point performance simulation[J]. Journal of Engineering for Gas Turbines and Power,2006,128(4): 789-795. [24] 程都. 基于神经网络的航空发动机模型自适应修正[D]. 辽宁 大连: 大连理工大学,2019. CHENG Du. Adaptive correction of aeroengine model based on neural network[D]. Dalian,Liaoning: Dalian University of Technology,2019. (in ChineseCHENG Du. Adaptive correction of aeroengine model based on neural network[D]. Dalian, Liaoning: Dalian University of Technology, 2019. (in Chinese) [25] 鲁峰,黄金泉,仇小杰,等. 基于信息熵融合提取特征的发动机气路分析[J]. 仪器仪表学报,2012,33(1): 13-19. LU Feng,HUANG Jinquan,QIU Xiaojie,et al. Feature extraction based on information entropy fusion for turbo-shaft engine gas-path analysis[J]. Chinese Journal of Scientific Instrument,2012,33(1): 13-19. (in ChineseLU Feng, HUANG Jinquan, QIU Xiaojie, et al. Feature extraction based on information entropy fusion for turbo-shaft engine gas-path analysis[J]. Chinese Journal of Scientific Instrument, 2012, 33(1): 13-19. (in Chinese) -
下载:
点击查看大图
计量
- 文章访问数: 131
- HTML浏览量: 70
- PDF量: 25
- 被引次数: 0