动力学相似准则和相似性设计方法是航空发动机转子系统研制的支撑技术。在以往的航空发动机转子动力学设计中，一般遵循避开临界转速的裕度准则，即按照“避开共振”的原则进行设计。因此，转子的动力学相似准则主要考虑无阻尼转子系统的模态相似性，即振型和临界转速的相似性，而一般不考虑阻尼以及不平衡响应的相似关系。

近年来，随着对战机战术要求的提升和飞行任务的多样性，高性能航空发动机在工作期间，转子频繁越过若干阶临界转速，甚至运行在临界转速位置或其邻域，难以保证工作转速与临界转速之间的裕度要求。简言之，转子要能够“容忍共振”。在此情况下，阻尼器的设计至关重要。为此，文献[1]提出了转子系统“可容模态”设计方法，即转子系统能够“容忍共振”的设计方法，强调阻尼器设计是“可容模态”设计的核心要素之一。这就要求转子在进行相似设计的过程中不仅要求振型和临界转速的相似性，还要求阻尼的相似性，一般来说对于挤压油膜阻尼器（squeeze film damper, SFD）提供的阻尼占到转子系统总阻尼的60%以上^[2]，即挤压油膜阻尼器提供的阻尼是航空发动机阻尼的关键构成部分，因此，带有挤压油膜阻尼器转子系统的相似性设计准则和相似设计方法是将实验验证结果向真实发动机移植的基础^[3]。

关于转子结构的动力学相似设计和带有挤压油膜阻尼器的转子系统动力学特性，国内外学者均作了大量的研究。袁文忠分析了相似理论在静力学模型实验中的应用，论述了小比例模型和大比例模型在相似后由于材料性能变化产生的相似误差，为保证误差相似模型和原型系统的尺寸差异不宜过大^[4]。王永亮等以量纲分析法为基础建立了考虑陀螺效应的转子动力学相似准则，验证了转子在考虑陀螺力矩的情况下，同时缩放转子尺寸和临界转速，转子动力学上仍能保持相似^[5]。罗忠等根据量纲分析理论建立了转子系统轴承支承刚度的相似关系，尽量选择符合相似参数的轴承设计了一个临界转速相似比为1∶1的相似模型，并同原型进行了仿真和实验对比分析，总结了转子系统前4阶临界转速的误差情况，达到了低于9.45%的实验误差^[6]。Harris等提出了转子振型置信度（MAC）作为转子振型相似度的评价函数，解决了前文所述相似研究中仅对比临界转速误差的问题^[7]。 Wu等研究了一个1/3缩比模型在相似激振力下的振动情况，比较了两转子振动特性关于时间的相似性^[8]。

上述的研究均集中在以转子结构几何相似为基础的动力学特性相似上，主要包括临界转速、模态振型和应变能的相似性。然而，关于目前航空发动机上最常用的阻尼结构-挤压油膜阻尼器的相似性设计研究甚少，使得模拟转子实验研究结果向发动机转子系统推广应用时，依据不够充分，存在不确定性。

郭银朝、孟光等以带有挤压油膜阻尼器的Jeffcott转子为研究对象，研究了阻尼器的油膜减振机理、转子系统的不平衡响应特性以及挤压油膜阻尼器的非线性特性，推导出引入油膜力后会使转子的幅频曲线展现出硬弹簧特性，该现象达到一定程度时就会出现双稳态响应^[9-10]。刘方杰等针对挤压油膜阻尼器的失效问题进行了理论分析和实验研究，提出应当匹配设计油膜间隙和目标不平衡量，控制偏心比达到防止挤压油膜阻尼器失效的目的^[11-12]。刘展翅研究了静偏心对挤压油膜阻尼器减振特性的影响，证明了挤压油膜阻尼器的工作特性与其偏心比相关，给出了挤压油膜阻尼器的线性工作区间。建立了挤压油膜阻尼器长轴承理论下和短轴承理论下不同油膜条件下的油膜力和阻尼模型，并对带挤压油膜阻尼器的实验转子进行了“可容模态”设计，并进行了转子 “容忍共振”的实验验证^[2,13]。上述的研究均未涉及带有挤压油膜阻尼器的转子系统动力学相似性设计内容，但明确了带有挤压油膜阻尼器的转子系统中的挤压油膜阻尼器相似设计应从转子系统和不平衡量的相似性入手，在考虑双稳态和硬弹簧特性的情况下结合油膜力模型进行分析推导。

为此，本文以转子动力学方程分析法为基础，从转子阻尼值的相似和挤压油膜阻尼器内部参数的相似两部分对带有挤压油膜阻尼器转子系统的相似性进行分析，提出挤压油膜阻尼器动力学相似准则和相似性设计方法，并通过仿真计算进行验证。

1.   挤压油膜阻尼器模型和油膜力

当计算转子的不平衡响应时，需要考虑在不同振动位移下挤压油膜阻尼器提供的阻尼。对于挤压油膜阻尼器，主要考虑4种工况下的阻尼，分别为带有端封的全油膜工况和带有端封的半油膜工况，以及无端封的全油膜工况和无端封的半油膜工况^[2]。

带挡油板或者O型圈等端封结构的挤压油膜阻尼器，一般使用长轴承假设计算其油膜力。在使用该模型时，视油膜轴向压力梯度为零，当阻尼器中油膜完全形成时，全油膜模型给出的稳态径向油膜力${F_{\rm{r}}}$和周向油膜力（tangential force）${F_{\rm{t}}}$如式（1）、式（2）所示^[14]。为区分挤压油膜阻尼器的尺寸参数和转子的尺寸参数，挤压油膜阻尼器的尺寸参数统一用下标表示。

应用半油膜模型时，稳态径向和周向油膜力分别如式（3）和式（4）所示

对于不带端封结构的挤压油膜阻尼器，一般根据短轴承假设来计算油膜力。在短轴承假设条件下，稳态全油膜径向油膜力和周向油膜力如下：

而据半油膜模型，稳态油膜力如式（7）和式（8）所示

式（1）～式（8）中$\,\mu$为滑油的黏度，主要由滑油种类和温度等因素决定，$\varOmega$为转子的稳态转速，${L_{\rm{c}}}$为油膜长度，${R_{\rm{c}}}$为油膜半径，${C_{\rm{r}}}$为油膜间隙，${\varepsilon _{\rm{c}}}$为在特定振动状态下的轴颈偏心比，${\varepsilon _{\rm{c}}} = e/{C_{\rm{r}}}$，$e$为轴颈偏心距。

由式（1）～式（8）可知，在挤压油膜阻尼器的几何结构确定后，挤压油膜阻尼器的油膜力仅与转速和轴颈偏心比相关，且与偏心比呈非线性关系。而轴颈偏心比由转子振动所决定。因此，挤压油膜阻尼器的油膜力与转子振动呈非线性关系。当挤压油膜阻尼器偏心比较小时，油膜力基本随偏心比线性变化；当偏心比达到一定值后，随着偏心比的增大油膜力的非线性逐渐增强。当偏心比趋向1时，挤压油膜阻尼器的切向油膜力和径向油膜力趋向无穷大。因此，在分析挤压油膜阻尼器相似关系时，需要考虑其非线性特性。

2.   转子系统阻尼和挤压油膜阻尼器的相似关系

2.1   带有阻尼的转子系统相似关系

考虑阻尼时，任一变截面转子的振动微分方程可以表示为^[1]

式中$E$为转子材料弹性模量，$I$为截面矩，$Z$为转子的径向位移，$x$为微元段轴向位置，$U$为转子的单位质量，$c$为转子在微元段处的阻尼，$\varOmega$为转子的稳态转速，$\varepsilon$为转子的质量偏心距，$\,\beta$为偏心距的相角，$t$为时间变量。

假设系统1与系统2之间存在如表1所示的参数关系。

表  1  相似关系表

Table  1.  Similarity relationship list

参数名称	参数符号		相似关系	参数间的关系
	系统1	系统2
材料弹性模量	$E'$	$E$	$E' = {\lambda _{{E} } }E$
材料密度	$\,\rho '$	$\,\rho$	$\,\rho ' = {\lambda _{\rho } }\rho$
径向尺寸	$d'$	$d$	$d' = {\lambda _{{d} } }d$
振动幅值	$Z'$	$Z$	$Z' = {\lambda _{{Z} } }Z$	${\lambda _{{d} } } = {\lambda _{{Z} } }$
偏心量	$\varepsilon '$	$\varepsilon$	$\varepsilon'= {\lambda _{{\varepsilon }}}\varepsilon$	${\lambda _{ {\varepsilon } } } = {\lambda _{{d} } } = {\lambda _{{Z} } }$
长度	$l'$	$l$	$l' = {\lambda _{{l} } }l$
轴向位置	$x'$	$x$	$x' = {\lambda _{{x} } }x$	${\lambda _{{x} } } = {\lambda _{{l} } }$
临界转速	$\omega '$	$\omega$	$\omega ' = {\lambda _{\omega} }\omega$
转子转速	$\varOmega '$	$\varOmega$	$\varOmega ' = {\lambda _{ {\varOmega } } }\varOmega$	${\lambda _{ {\varOmega } } } = {\lambda _{\omega } }$
时间	$t'$	$t$	$t' = {\lambda _{{t} } }t$
质量	$m'$	$m$	$m' = {\lambda _{{m} } }m$
单位长度质量	$U'$	$U$	$U' = {\lambda _{{U} } }U$	${\lambda _{{U} } } = {\lambda _{{m} } }\lambda _{{x} }^{ {{ - 1} } } = {\lambda _{\rho } }\lambda _{{d} }^{{2} }$
转动惯量	$I'$	$I$	$I' = {\lambda _{{I} } }I$	${\lambda _{{I} } } = \lambda _{{d} }^{{4} }$

下载: 导出CSV 

| 显示表格

表1中带有角标的变量为系统1的参数，无角标的变量为系统2的参数，$\lambda$代表下标对应参数之间的相似比。

由于转子轴向尺寸和轴向位置的相似比是一致的，故${\lambda _{{x}}} = {\lambda _{{l}}}$。另外，转子的转速需要与转子的临界转速成比例，故有$\varOmega '/\varOmega = {\lambda _{\rm{\varOmega }}} = \omega '/\omega = {\lambda _{\omega}}$。转子单位长度内的质量相似关系为${\lambda _{{U}}} = {\lambda _{{m}}}\lambda _{{x}}^{ - 1} = {\lambda _{\rho}}\lambda _{{d}}^2$。此外，根据转子结构的几何相似关系，截面矩与径向尺寸之间的相似关系为${\lambda _{{I}}} = \lambda _{{d}}^{{4}}$。

对于几何相似的系统1和系统2，系统1的振动微分方程可以用系统2的参数来表示，即

如果方程中的阻尼项$c （x） =0$，为使该微分方程仍然成立，则式（10）各转子参数项前的相似系数项应当相等，即

但对于有阻尼系统，即$c （x） \ne 0$的情况下，转子的振动幅值与转子随时间的运行状态变化情况相关，此时，相似关系式需要同时满足式（10）的系数相等条件，以及转速和时间相似比条件，如式（12）所示。

将表1中的相似比关系以及前文所述的截面矩与径向尺寸的相似关系式代入式（12），并进行整理，可以得到转子的转速-时间相似关系，如式（13）所示。

同样利用表1中相似比关系，利用式（12）第一行前两项，并代入式（13）可以推导出转子阻尼相似关系式，如式（14）所示。

由于系统1与系统2的转速和质量均不相同，对于一对相似系统而言，假设系统1在转速$\varOmega$达到振动幅值A时，对应的不平衡量为${U_{\rm{b}}}$；系统2在转速$\varOmega '$达到振动幅值$A '$时，不平衡量为${U'_{\rm{b}}}$，对应的相似比为${\lambda _{{\rm{ub}}}}$。根据上述推导可知，不平衡量与其他参数相似比之间的关系为

可以推导得出不平衡力$f$其他参数相似比之间的关系${\lambda _f}$为

2.2   挤压油膜阻尼器参数相似关系

文中第2.1节通过分析带有阻尼的转子系统的振动微分方程，得到了阻尼值与转子几何参数之间的相似关系。一般来说，发动机转子的阻尼主要由挤压油膜阻尼器产生。因此，在发动机设计中，需要将转子参数与阻尼值的相似关系映射到阻尼值与挤压油膜阻尼器的内部参数之间的相似关系上。

挤压油膜阻尼器提供的油膜阻尼随着轴颈偏心比的变化而变化，在长轴承假设下，根据式（1）～式（4），挤压油膜阻尼器的阻尼力可以整理成如下的形式：

在短轴承假设下，根据式（5）～式（8），挤压油膜阻尼器的阻尼力可表示为

式中$N$为油膜力系数，${E_{\rm{c}}}$为偏心比系数，表达式为E_c=ε/C_r， 两者均为无量纲量。

对于几何相似的系统1和系统2，系统1的挤压油膜阻尼器内部参数和油膜力之间的关系可以用系统2的参数关系来表示，如表2所示。

表  2  挤压油膜阻尼器参数相似关系表

Table  2.  Similarity relationship list of SFD parameters

参数名称	参数符号		相似关系
	系统1	系统2
滑油黏度	$\,\mu '$	$\,\mu$	$\,\mu ' = {\lambda _{\mu} }\mu$
油膜长度	${L'_{\text{c} } }$	${L_{\text{c}}}$	${L'_{\text{c} } } = {\lambda _{ { { {L} }_{\text{c} } } } }{L_{\text{c} } }$
油膜半径	${R'_{\text{c} } }$	${R_{\text{c}}}$	${R'_{ {\text{c} } } } = {\lambda _{ { { {R} }_{\text{c} } } } }{R_{\text{c} } }$
油膜间隙	${C'_{\text{r} } }$	${C_{\text{r}}}$	${C'_{\text{r} } } = {\lambda _{ { { {C} }_{\text{r} } } } }{C_{\text{r} } }$

下载: 导出CSV 

| 显示表格

因此，长轴承假设下挤压油膜阻尼器的内部相似参数关系可以表示为

短轴承假设下挤压油膜阻尼器的内部相似参数关系可以表示为

为保证式（19）、式（20）成立，首先要保证无量纲的油膜力系数N、偏心比系数${E_{\rm{c}}}$相等，即

这要求系统1和系统2的挤压油膜阻尼器工作状态相同，即挤压油膜阻尼器的端封条件、油膜形成状态相同。

同时，转子的轴颈偏心比也须相同。满足该条件需要保证轴颈偏心量的相似比与油膜间隙的相似比保持一致，即

由于转子系统中所有力参数的量纲是相同的，因此，油膜力相似比${\lambda _{{\rm{fc}}}}$应与不平衡力相似比${\lambda _{\rm{f}}}$相同。其中基于长轴承假设的相似比之间的关系如式（23）所示：

短轴承假设下的相似比之间的关系如式（24）所示。

进一步推导可得长轴承假设下挤压油膜阻尼器的油膜半径、油膜长度与其余转子参数相似比之间的关系式如式（25）所示。

相应地短轴承假设下挤压油膜阻尼器的油膜半径、油膜长度与其余转子参数相似比应满足如下的关系：

如果两个相似系统采用的滑油黏度相同，即滑油黏度相似比等于1，则式（25）和式（26）分别退化为

由式（27）、式（28）可见，挤压油膜阻尼器的油膜长度和油膜半径构成了一个组合参数，该组合参数则可由转子的材料相似参数和几何相似参数共同确定。这是转子挤压油膜阻尼器动力学相似设计的准则。

如果可按照转子系统的径向尺寸相似比设计挤压油膜阻尼器的油膜半径，即${\lambda _{{R_{\rm{c}}}}} = {\lambda _d}$时，可以直接由式（29）、式（30）得到油膜长度的相似比。长轴承假设下挤压油膜阻尼器的油膜长度与其余参数相似比之间的关系为

相应地，短轴承假设下挤压油膜阻尼器的油膜长度与其余参数相似比之间的关系为

3.   挤压油膜阻尼器内部参数相似性设计

在发动机研制过程中，往往是首先利用实验模拟转子对发动机转子系统的动力学设计进行初步的验证和改进。在此基础上，再进行下一轮的设计和真实部件的验证。因此，动力学特性相似，包括挤压油膜阻尼器特性的相似非常重要。为说明挤压油膜阻尼器相似设计的流程和方法，不妨定义转子系统1为实验模拟转子，转子系统2为发动机转子。

3.1   挤压油膜阻尼器相似设计流程

根据相似理论，带有挤压油膜阻尼器的转子系统动力学相似设计主要分为5个步骤。①选取合适的相似参数，根据系统2的尺寸得到系统1的尺寸，以及在挤压油膜阻尼器处的轴颈半径和振动幅值相似比。②根据振动幅值相似比设计相似的挤压油膜阻尼器油膜间隙，由此，就保证了挤压油膜阻尼器工作时的轴颈偏心比相同。③根据阻尼器处轴颈尺寸确认挤压油膜阻尼器处轴承型号，根据轴承外环直径和结构形式确定油膜半径。④根据油膜半径和油膜间隙相似比，计算挤压油膜阻尼器的油膜长度相似比，确定油膜长度尺寸。⑤根据系统1的实验结果对设计进行优化，利用文中第3节建立的相似理论反推系统2的结构尺寸。

上述过程对于无畸变的转子相似设计来说，可以按照要求，一次计算出对应的阻尼器结构。对于带有畸变的转子结构，可以参照文献[15]，利用遗传算法或粒子群算法等优化算法对转子的振型和不平衡响应进行迭代优化。

3.2   挤压油膜阻尼器的相似性设计

在上述的理论推导中，挤压油膜阻尼器相似参数的取值范围相对较大，各个参数相对独立，理论上能够较好地实现转子系统1与转子系统2之间的相似。然而在实际发动机转子系统动力学相似的设计中，由于结构原因，系统1与系统2难以按照无畸变的条件设计得完全相似，此时，可以根据实验验证的目的对阻尼相似性进行折中处理。

一般情况下，要求满足系统1即模拟实验转子设计要求的挤压油膜阻尼器，用在与之相似的系统2即发动机转子上，应当具有更高的阻尼比，同时临界转速和对应振型应当满足相似性。为此，需要保证系统2的阻尼比$C$大于等于系统1的阻尼比，还要保证包括油膜刚度在内的支承刚度保持相似，即须满足如下条件：

对于工作在全油膜状态下的挤压油膜阻尼器而言，其油膜刚度为零。因此，仅需要满足条件（式（31））中第一个条件即可。而对于工作在半油膜状态下的挤压油膜阻尼器，油膜会产生油膜刚度。但当挤压油膜阻尼器工作在线性区域时，油膜刚度最大一般仅占弹支刚度的5%。因此，即使不考虑油膜刚度也能够满足大多数工程应用要求。

如果在特定条件下需要验证系统1存在大油膜刚度的情况，即系统1的实验目的包括验证转子振动水平较高时挤压油膜阻尼器工作在非线性区域的特性。此时，油膜刚度的影响较为显著，需要将系统1的弹支刚度与油膜刚度综合考虑，使系统1的弹支刚度和油膜刚度的总和与系统2的总刚度（弹支刚度和油膜刚度的总和）保持相似，即满足式（31）的2个条件。对于工作在非线性区间的挤压油膜阻尼器，由于油膜刚度可能较大，调整弹支刚度会同时对临界转速和油膜刚度造成影响，因此，需要迭代计算系统1的弹支刚度及临界转速处的油膜刚度，迭代计算流程如图1所示。

图  1  迭代设计流程

Figure  1.  Iterative design process

下载: 全尺寸图片 幻灯片

3.3   实际应用中的考虑

在发动机中，${L_{\rm{c}}}/{R_{\rm{c}}} < 0.5$，大多数情况下，${L_{\rm{c}}}/{R_{\rm{c}}} < 1/3$。对带有端封的挤压油膜阻尼器，根据长轴承假设确定油膜阻尼，即利用式（2），或式（4）计算, 计算结果偏大。可应用文献[1]所介绍的有限长阻尼器模型进行修正。由于修正系数仅与偏心比有关，故修正结果并不影响本文所提出的相似理论。

也可根据短轴承假设和全油膜模型进行相似性设计，即式（6），而利用半油膜模型式（8）进行验证。在系统1上满足要求的阻尼器，在系统2上必会满足要求。这是由于发动机中阻尼器易于形成全油膜，全油膜的阻尼较半油膜大一倍，另外，阻尼器均带有端封，因此，这样的设计和验证方法偏于可靠和安全。

4.   动力学相似性验证

4.1   转子模型及其相似参数

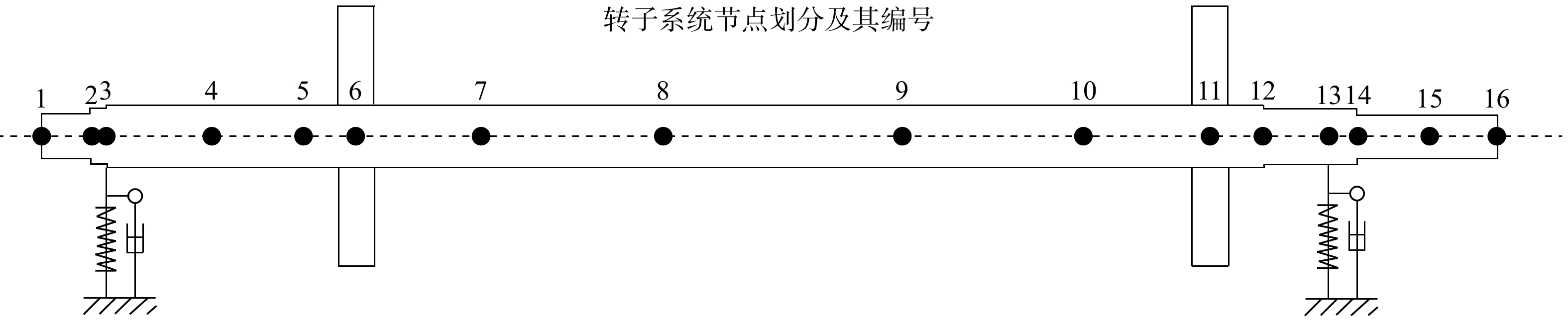
为验证本文提出的带挤压油膜阻尼器转子系统动力学相似性设计方法，取图2所示的转子系统作为验证示例。如图2所示，示例为一双盘简支转子，双盘在轴上采用非对称布局，两盘均为等厚圆盘，但质量和转动惯量不相同。支承也为非对称布置，前端的3号节点为带有鼠笼式挤压油膜阻尼器的弹性支承，其支承刚度主要由鼠笼弹支刚度决定，阻尼主要由挤压油膜阻尼器的参数决定，转子后端的13号节点为一刚性支承，其刚度和阻尼主要取决于轴承参数。

图  2  转子系统模型

Figure  2.  Model of rotor system

下载: 全尺寸图片 幻灯片

根据图2所示的转子模型节点划分，利用有限元法建立转子系统的振动微分方程如下^[16-18]：

式中${{\boldsymbol{M}}}$为转子系统的质量矩阵，${\boldsymbol{C}}$为转子系统的阻尼矩阵，${\boldsymbol{G}}$为系统的陀螺力矩矩阵，${{\boldsymbol{K}}}$为系统的刚度矩阵，${\boldsymbol{Q}}$为系统的外力，在本文的分析中，系统的外力向量为转子的不平衡力向量，${\boldsymbol{q}}$为系统的广义坐标向量，${{\boldsymbol{\varOmega}} }$代表计算时刻转子的转速。

对上述微分方程进行求解可以得到转子的各阶模态。

利用文中第2.2节推导得出的相似关系，将图2所示的转子系统定义为原型系统即系统2，建立其缩比的相似系统1。系统1的长度和径向尺寸均为系统2的0.8，各部件材料保持不变。根据文中第2节中的关系式，可得系统1的临界转速为系统2的1.25倍。采用短轴承假设下的挤压油膜阻尼器进行相似计算，取径向尺寸相似比与转子相同，为0.8，按照式（28）计算出挤压油膜阻尼器轴向长度相似比为0.7427。系统1和系统2各个参数采用的相似比如表3所示。

表  3  相似参数表

Table  3.  Similarity parameters list

相似参数	相似比符号	相似比
弹性模量	${\lambda _{{E} } }$	1
密度	${\lambda _{\rho } }$	1
轴向尺寸	${\lambda _{{l} } }$	0.8
径向尺寸	${\lambda _{{d} } }$	0.8
偏心量	${\lambda _{{\varepsilon }}}$	0.8
转速	${\lambda _{\omega}}$	1.25
阻尼值	${\lambda _{{c} } }$	0.64
不平衡质量	${\lambda _{\rm{ub}}}$	0.4096
滑油黏度	${\lambda _{\mu } }$	1
油膜长度	${\lambda _{ {{L_{\rm{c}}} } } }$	0.7427
油膜半径	${\lambda _{ { {{R} }_{\text{c} } } } }$	0.8

下载: 导出CSV 

| 显示表格

根据上述相似参数，设计系统1与系统2相似，系统1和系统2的转子部分的主要参数如表4所示。

表  4  转子系统主要参数

Table  4.  Main parameters of rotor system

参数	系统1	系统2
主轴长度/m	0.644	0.805
支承跨距/m	0.5408	0.676
主轴半径/m	0.0264	0.033
盘1质量/kg	8.3507	16.31
盘2质量/kg	9.7024	18.95
盘1极转动惯量/（kg·m2）	0.0452	0.138
盘2极转动惯量/（kg·m2）	0.0609	0.186
1号支承刚度/109 （N/m）	0.8	1

下载: 导出CSV 

| 显示表格

相应地，根据挤压油膜阻尼器相似关系计算得出的挤压油膜阻尼器相似参数如表5所示。

表  5  挤压油膜阻尼器主要参数

Table  5.  Main parameters of SFD

参数	系统1	系统2
2号支承刚度/106 （N/m）	2.6	3.2
油膜长度/m	0.0074	0.01
油膜半径/m	0.054	0.0675
油膜间隙/m	0.000128	0.00016
油膜间隙比/‰	2.37	2.37

下载: 导出CSV 

| 显示表格

4.2   转子振型相似度验证

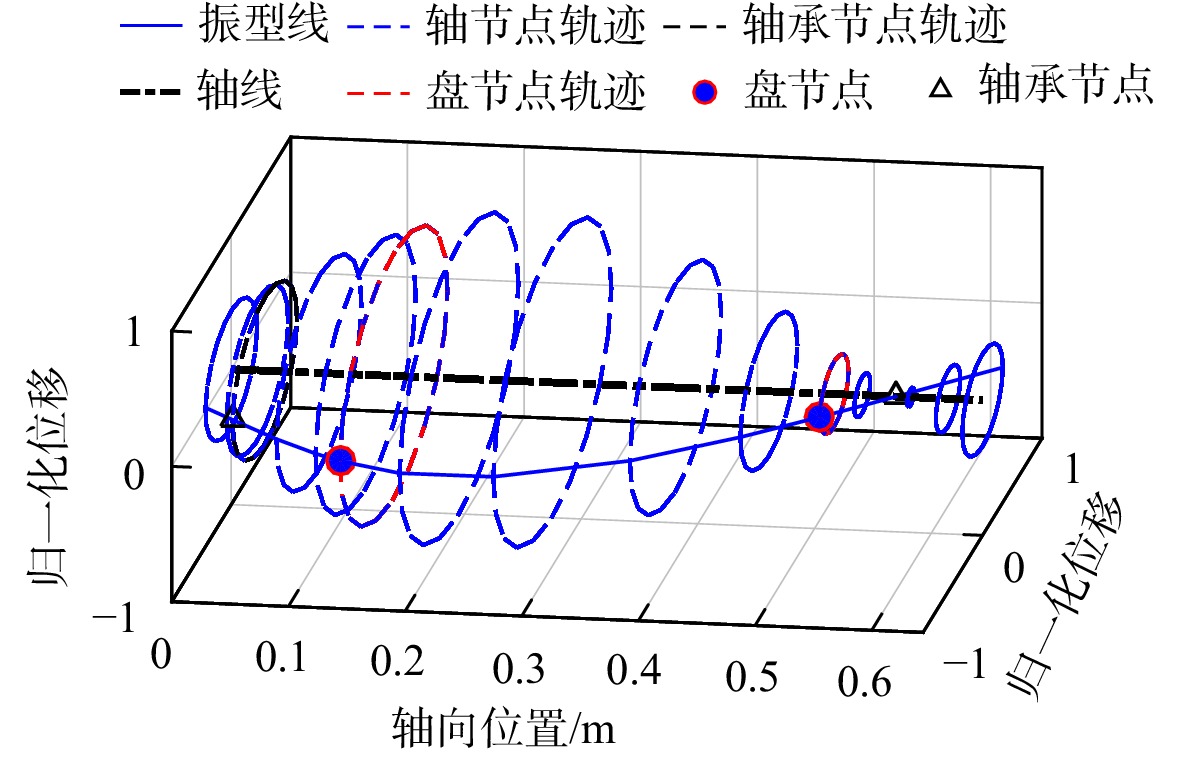
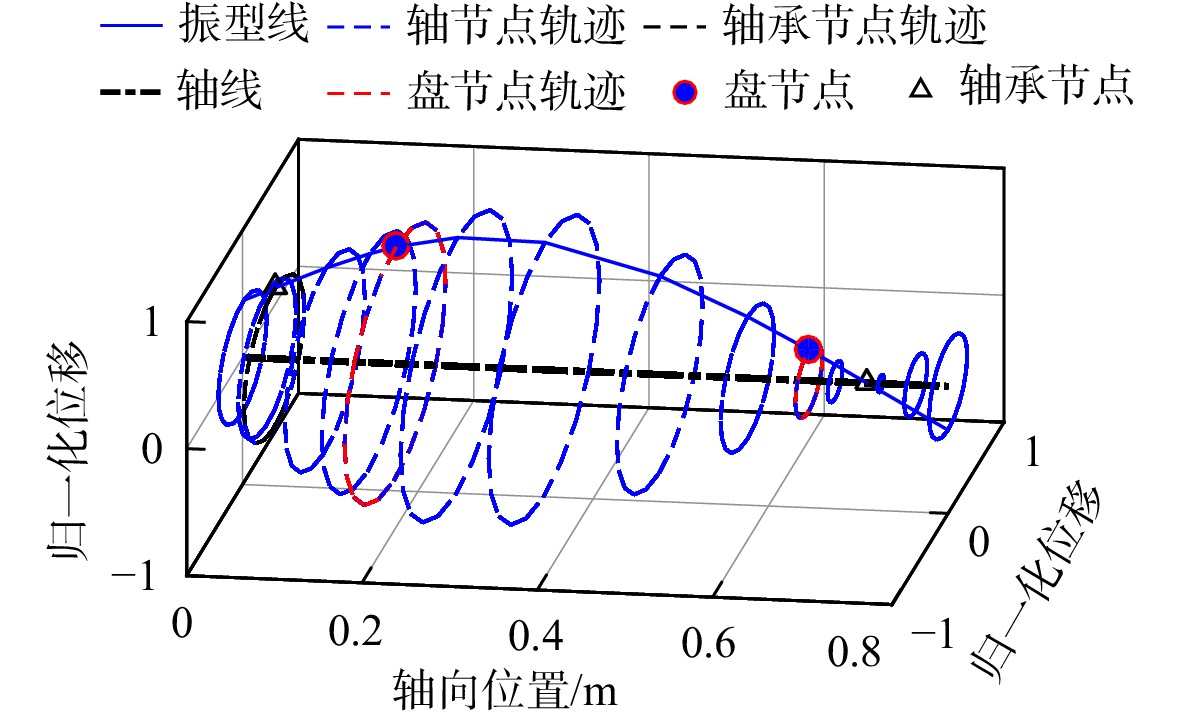
利用有限元法分别计算系统1与系统2的1阶振型及其临界转速。系统1的1阶模态振型如图3所示，对应的临界转速为4212.4 r/min。系统2的1阶模态振型如图4所示，对应的临界转速为3369.9 r/min。系统1与系统2的振型除初始相位不同外，振型高度一致，振型置信度为1。计算得出的1阶模态临界转速相似比为1.25，与设定的相似比相同。

图  3  系统1模态振型

Figure  3.  Mode vibration shape of system 1

下载: 全尺寸图片 幻灯片

图  4  系统2模态振型

Figure  4.  Mode vibration shape of system 2

下载: 全尺寸图片 幻灯片

4.3   线性阻尼下转子不平衡响应验证

计算系统1和系统2在线性恒定阻尼作用下的不平衡响应。在系统2盘1处加上许用不平衡量15 g·cm，相应地，根据相似比计算可知，应在系统1的盘1处施加6.144 g·cm的不平衡量。在系统2所有轴承处施加1000 N·s/m 阻尼，通过相似比计算可知，系统1的相似阻尼值为640 N·s/m 阻尼。

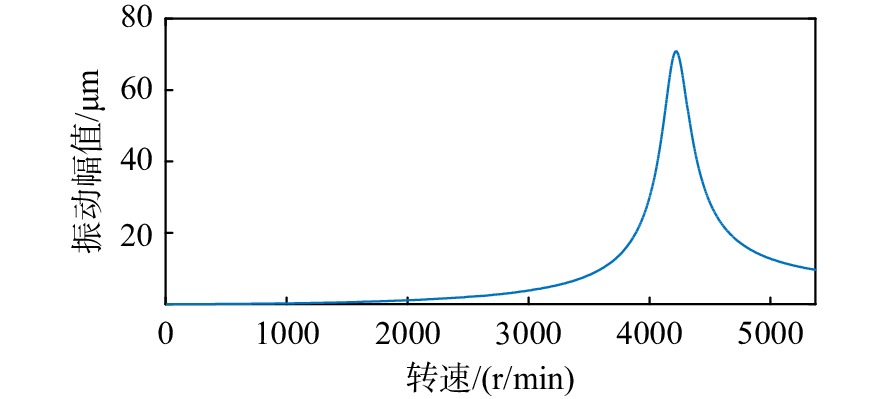
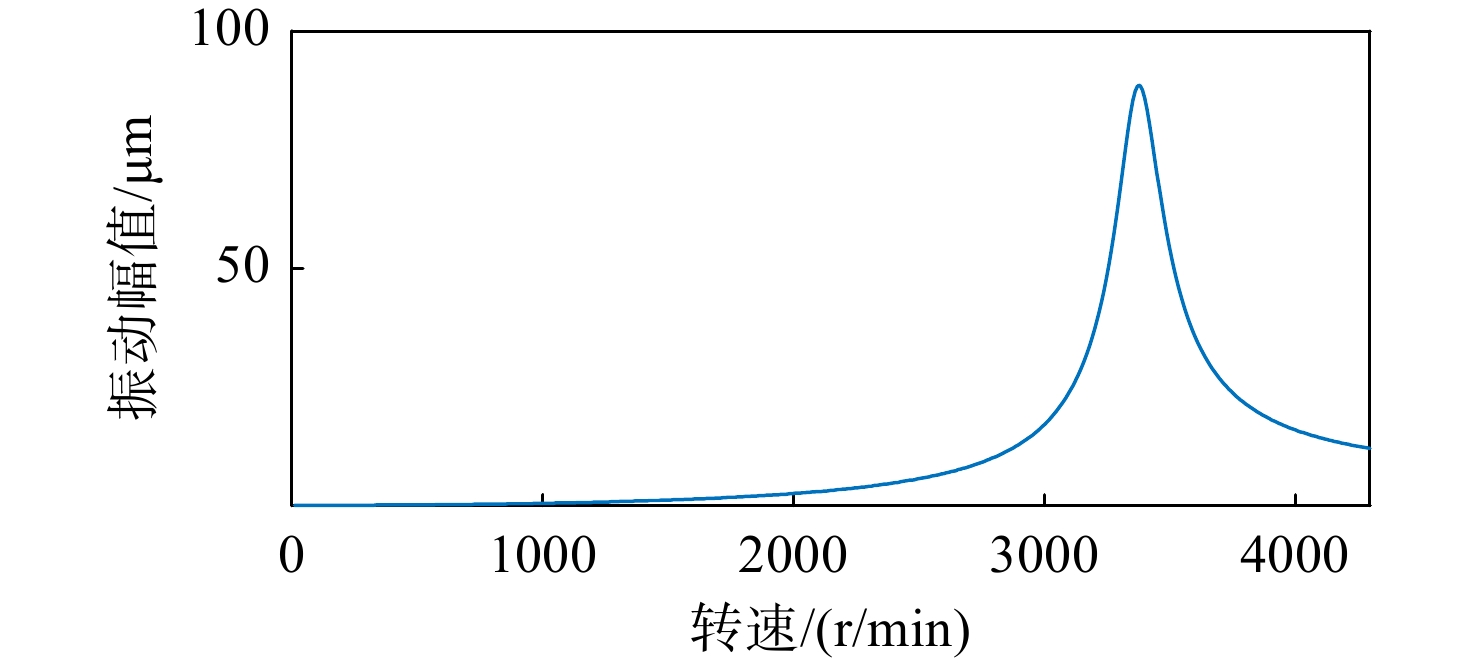
分别计算系统1和系统2的不平衡响应，结果如图5和图6所示。系统1在4221 r/min 处达到响应峰值70.94 μm，系统2在3376 r/min 处达到响应峰值88.58 μm。响应峰值对应的转速比为1.25，响应幅值即偏心量的相似比为0.80。转子关键参数及其相似比情况如表6所示，符合相似性设计结果。

图  5  线性阻尼下系统1不平衡响应

Figure  5.  Unbalance response under linear damping of system 1

下载: 全尺寸图片 幻灯片

图  6  线性阻尼下系统2不平衡响应

Figure  6.  Unbalance response under linear damping of system 2

下载: 全尺寸图片 幻灯片

表  6  线性阻尼下的不平衡响应

Table  6.  Unbalance response of the rotor with linear damping

参数	系统1	系统2	参数目标相似比	参数实际相似比
不平衡量/（g·cm）	6.144	15	0.410	0.410
线性阻尼值/（N·s/m）	640	1000	0.64	0.64
响应峰值转速/（r/min）	4221	3376	1.25	1.25
响应峰值/μm	70.94	88.58	0.80	0.80

下载: 导出CSV 

| 显示表格

4.4   挤压油膜阻尼器作用下转子不平衡响应验证

现计算系统1和系统2在挤压油膜阻尼器作用下的不平衡响应。在系统1的盘1处施加2.048 g·cm 的不平衡量，按照相似比，在系统2的盘1处施加5 g·cm 的不平衡量。取短轴承假设下的半油膜模型，计算挤压油膜阻尼器的刚度和阻尼。如图7所示，系统1在4238 r/min 处, 响应达到峰值，峰值处挤压油膜阻尼器轴颈偏心比为0.1679，不平衡响应振动峰值为21.49 μm。图8则表示，系统2在3390 r/min 处, 响应达到峰值，峰值处挤压油膜阻尼轴颈偏心比为0.1674，不平衡响应振动峰值为26.78 μm。响应峰值对应的转速比为1.25，偏心比相似误差0.299%，无量纲阻尼系数均约为1.639，响应幅值相似比为0.80。关键相似参数及其目标参数比与实际参数比之间的关系如表7所示。上述计算结果表明，文中第3节所建立的挤压油膜阻尼器相似性设计方法是有效的。

图  7  挤压油膜阻尼器线性状态下系统1偏心比

Figure  7.  Eccentricity ratio of system 1 under linear state of SFD

下载: 全尺寸图片 幻灯片

图  8  挤压油膜阻尼器线性状态系统2偏心比

Figure  8.  Eccentricity ratio of system 2 under linear state of SFD

下载: 全尺寸图片 幻灯片

表  7  挤压油膜阻尼器线性状态下的不平衡响应信息

Table  7.  Unbalance response information under linear state of SFD

参数	系统1	系统2	参数目标相似比	参数实际相似比
不平衡量/（g·cm）	2.048	5	0.410	0.410
响应峰值转速/（r/min）	4238	3390	1.25	1.25
响应峰值/μm	21.49	26.78	0.800	0.802
偏心比峰值	0.1679	0.1674	1.000	1.003
无量纲阻尼系数	1.639	1.639	1.00	1.00

下载: 导出CSV 

| 显示表格

4.5   挤压油膜阻尼器非线性阻尼下转子的双稳态响应验证

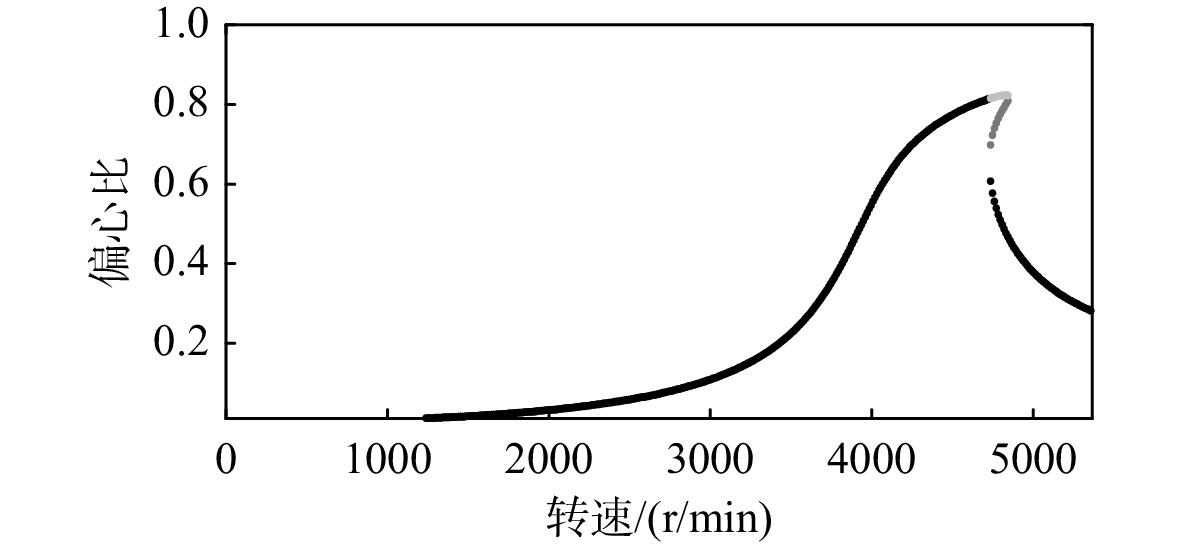
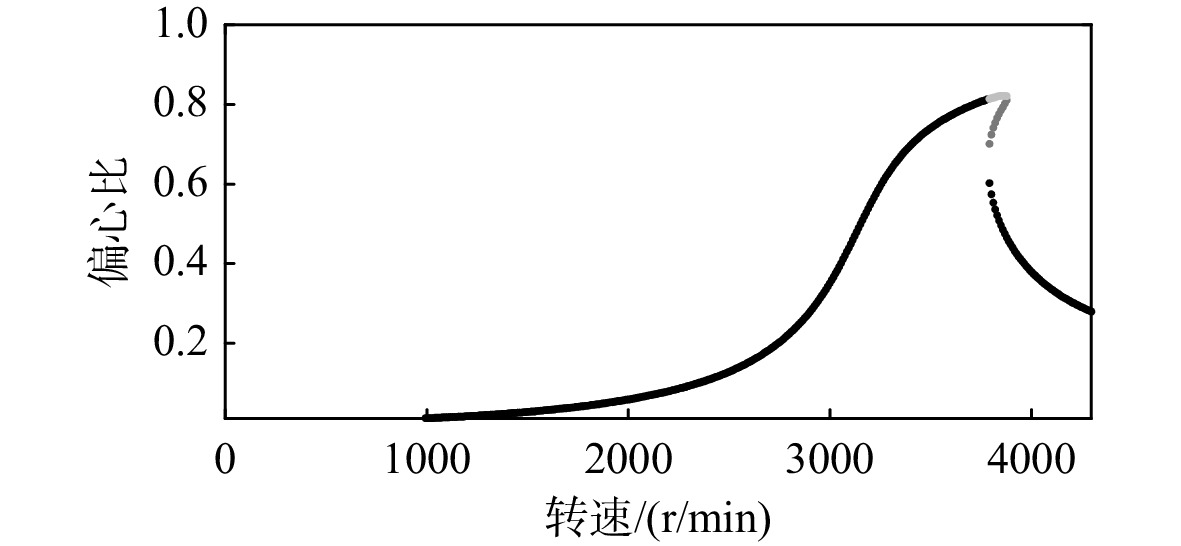
当转子的振动过大时，挤压油膜阻尼器的轴颈偏心比会相应增大，转子的振动响应会表现出强烈的非线性。转子的双稳态响应是挤压油膜阻尼器在非线性区间工作时的典型振动现象。在双稳态现象出现的转速范围内，转子的幅值和相位均有3个解，其中最大解和最小解为稳定解。当转子增速时，转子运行在最大解的轨道上，当转子减速时转子运行在最小解轨道上。分别计算当挤压油膜阻尼器工作在非线性区域时系统1和系统2的双稳态响应。在系统1的盘1处施加22.528 g·cm 的不平衡量，根据相似比，在系统2的盘1处施加55 g·cm的 不平衡量，仍取短轴承假设下的半油膜模型，计算挤压油膜阻尼器的刚度和阻尼。系统1和系统2的偏心比随转速的变化如图9和图10所示。

图  9  SFD非线性状态系统1偏心比

Figure  9.  Eccentricity ratio under SFD nonlinear state of system 1

下载: 全尺寸图片 幻灯片

图  10  SFD非线性状态系统2偏心比

Figure  10.  Eccentricity ratio under SFD nonlinear state of system 2

下载: 全尺寸图片 幻灯片

双稳态下挤压油膜阻尼器的参数和转子响应参数对比如表8所示。表8分别列出了系统1和系统2进、出双稳态的转速范围，增速过程中进、出双稳态的偏心比（即最大解序列），减速过程中进、出双稳态的偏心比（即最小解序列），以及最大轴颈位移。轴颈偏心比最大计算误差为0.831%，共振转速相似比为1.25,响应峰值相似比为0.80。

表  8  挤压油膜阻尼器双稳态信息

Table  8.  SFD bi-stable information

参数	系统1	系统2	参数目标相似比	参数实际相似比
最低转速/（r/min）	4736	3791	1.25	1.249
最高转速/（r/min）	4844	3877	1.25	1.249
最低转速最大偏心比	0.815	0.814	1	1.001
最高转速最大偏心比	0.823	0.821	1	1.002
最低转速最小偏心比	0.467	0.465	1	1.004
最高转速最小偏心比	0.607	0.602	1	1.008
响应峰值	105.2 μm	131.2 μm	0.8	0.802

下载: 导出CSV 

| 显示表格

计算结果证明了文中第3节所述的挤压油膜阻尼器相似理论能够保证挤压油膜阻尼器双稳态现象的相似性，系统1和系统2具有相似的双稳态转速范围，以及偏心比最大解和最小解。

4.6   全油膜相似与半油膜相似对比

本文中第3.3节中提出在实际应用中可以考虑令系统2工作在全油膜状态下，令系统1工作在半油膜状态下，从而保证在对应的相似转速下系统1的油膜阻尼始终小于系统2的油膜阻尼，提高设计和验证方法的可靠性和安全性。当挤压油膜阻尼器工作在全油膜状态下时，系统2在15 g·cm不平衡量激励下的不平衡响应如图11所示。相应地，系统1在相似的6.144 g·cm 不平衡量下不平衡响应如图12所示。图12中橙色虚线代表全油膜状态下的不平衡响应，与图11中的状态相似。蓝色实线代表半油膜状态下的不平衡响应，可见半油膜状态下系统1的不平衡响应大于全油膜状态下的不平衡响应，即半油膜状态下阻尼器提供的阻尼低于全油膜状态下阻尼器提供的阻尼。因此，可根据短轴承假设和全油膜模型进行相似性设计，而利用半油膜模型进行验证。此时，在系统1上满足要求的阻尼器，在系统2上必会满足要求。

图  11  系统2全油膜不平衡响应

Figure  11.  Unbalance response under non-cavitated film of system 2

下载: 全尺寸图片 幻灯片

图  12  系统1全油膜与半油膜状态不平衡响应对比

Figure  12.  Unbalance response under non-cavitated and cavitated oil film of system 1

下载: 全尺寸图片 幻灯片

5.   与现有挤压油膜阻尼器设计理论的对比

航空发动机设计手册^[19]给出了挤压油膜阻尼器油膜间隙比的推荐取值范围，即2‰～5‰。目前已较广泛地应用于航空发动机转子的设计中。但这一取值范围是否满足动力学相似的要求，尚未见证明。另外，取值范围偏大，往往不易掌握。关于油膜长度尚无清晰的设计规范。

现将本文建立的挤压油膜阻尼器动力学相似设计方法与目前的设计规范进行比较。

根据文中第3.3节所提出的挤压油膜阻尼器设计方法，由转子轴颈偏心比相同可直接得出挤压油膜阻尼器的油膜间隙。由式（25）和式（26）可知，挤压油膜阻尼器的油膜长度比和油膜半径比构成的组合参数由转子系统材料和几何相似比所决定。可按照转子结构几何相似比确定油膜半径。此时，利用式（27）或式（28）确定油膜长度比。验证示例的设计结果如表4所示，系统1的油膜半径为0.054 m，油膜长度为0.0074 m，油膜间隙比为2.37‰。系统2的油膜半径为0.0675 m，油膜长度为0.01 m，油膜间隙比也为2.37‰。由此可见，按照本文提出的挤压油膜阻尼器动力学相似设计方法所设计的油膜间隙比落在目前设计规范所推荐的取值范围内。所设计的油膜长度在实际中也是可行的。需要注意的是，此处的油膜长度指的是净长度，不包括两端的密封槽。经过系统1验证后，在系统2中，可适当加长油膜长度，使得相似性设计更偏于安全。

根据挤压油膜阻尼器的周向力表达式，式（2）、式（4）、式（6）和式（8），可分别求得对应的阻尼系数如下：

长轴承假设全油膜模型的阻尼系数

长轴承假设半油膜模型的阻尼系数

短轴承假设全油膜模型的阻尼系数

短轴承假设半油膜模型的阻尼系数

式中${\bar C_{\rm{r}}} = {{{C_{\rm{r}}}}}/{{{R_{\rm{c}}}}}$为油膜间隙比。

由以上阻尼系数的表达式可见，油膜阻尼对油膜间隙比非常敏感。间隙越小，阻尼越大。但间隙过小，滑油难于进入油膜间隙，无法形成完整的油膜。因此，油膜间隙比的取值要考虑如下的因素：

1） 所取的最小间隙值应保证滑油能够进入间隙，形成完整的油膜。例如，航空发动机设计手册推荐的间隙比下限2‰主要就是考虑这一要求。

2） 能够满足动力学相似设计的要求，即在系统1验证有效的阻尼器参数，在与之动力学相似的系统2中也是有效的。本文提出的设计方法就可解决这一问题。

在阻尼系数的表达式（式（31）～式（34））中，均包含油膜间隙比的负三次方项，即$\bar C_{\rm{r}}^{{{ - 3}}}$。假设其他参数不变，当油膜间隙比从2‰增大到5‰时，挤压油膜阻尼器的阻尼会减小到原来的1/15。因此，利用本文建立的挤压油膜阻尼器相似性设计方法，进行预先设计是必要的。将此设计结果作为必要条件，在此基础上再进行优化。

6.   结　论

本文从转子运动微分方程出发，提出了带阻尼转子系统动力学相似的条件。根据挤压油膜阻尼器油膜力与参数间的关系，推导出由阻尼器油膜半径比和油膜长度比构成的组合参数与转子材料参数和几何参数相似比的关系，建立了带挤压油膜阻尼器转子系统相似性设计方法，并进行了仿真计算验证，得出以下结论：

1） 对有阻尼的转子系统只有当阻尼和结构材料、几何都满足相似准则的情况下才能动力学相似。

2） 通过理论推导证明了，若要挤压油膜阻尼器在转子系统动力学相似前后提供相似的阻尼，挤压油膜阻尼器的油膜间隙需要符合转子结构的几何相似关系，而油膜半径和油膜长度仅需要两者构成的组合参数满足对应的转子几何相似关系。

3） 如果润滑条件（滑油和温度）相同，可由油膜半径相似比和油膜长度相似比构成挤压油膜阻尼器的组合相似参数。该组合参数可由转子系统的材料参数相似比和几何尺寸相似比共同确定。若油膜半径由轴颈的几何相似确定时，油膜长度就可唯一地由转子系统的材料参数相似比和几何尺寸相似比确定。按照该方法设计挤压油膜阻尼器可保证两个转子系统的阻尼相似。

4） 可根据短轴承假设和全油膜模型进行相似性设计，而利用半油膜模型进行验证。在系统1上满足要求的阻尼器，在系统2上必会满足要求。这样的设计和验证方法偏于可靠和安全。

5） 将本文建立的挤压油膜阻尼器相似设计方法与航空发动机设计手册中关于挤压油膜阻尼器油膜间隙比的设计准则进行了对比和分析。结果表明，利用本文建立的挤压油膜阻尼器相似性设计方法，可较准确地确定油膜间隙比，保证阻尼器的动力学相似性。