基于EWT的离心压气机出口动态压力样本熵分析

刘雁; 李宇宸; 张赫; 肖军

doi:10.13224/j.cnki.jasp.20210509

基于EWT的离心压气机出口动态压力样本熵分析

doi: 10.13224/j.cnki.jasp.20210509

刘雁^1,,
李宇宸^1,*, ,,
张赫¹,
肖军²

1.
西北工业大学机电学院，西安 710072
2.
合肥通用机械研究院有限公司压缩机技术国家重点实验室，合肥 230031

基金项目: 国家自然科学基金（51775437）；压缩机技术国家重点实验室开放基金（SKL-YSJ201902）；国家重点研发计划（2019YFB1504601）

详细信息

作者简介:
刘雁（1974-），女，副教授，博士，研究方向为非线性动力学和动力系统稳定性。E-mail：liuyan@nwpu.edu.cn

通讯作者:
李宇宸（1998-），男，硕士生，研究方向为非线性动力学和动力系统稳定性。E-mail：liyuchen2059@outlook.com

中图分类号: V235.11
计量
- 文章访问数: 223
- HTML浏览量: 68
- PDF量: 187
- 被引次数: 0
出版历程
- 收稿日期: 2021-09-12
- 网络出版日期: 2023-01-08

Sample entropy characteristics of dynamic pressure at outlet of centrifugal compressor based on EWT

LIU Yan^1
,,
LI Yuchen^{1,*
, ,},
ZHANG He¹,
XIAO Jun²

1.
School of Mechanical Engineering， Northwestern Polytechnical University，Xi’an 710072，China
2.
State Key Laboratory of Compressor Technology， Hefei General Machinery Research Institute Company，Limited，Hefei 230031，China

摘要

摘要:
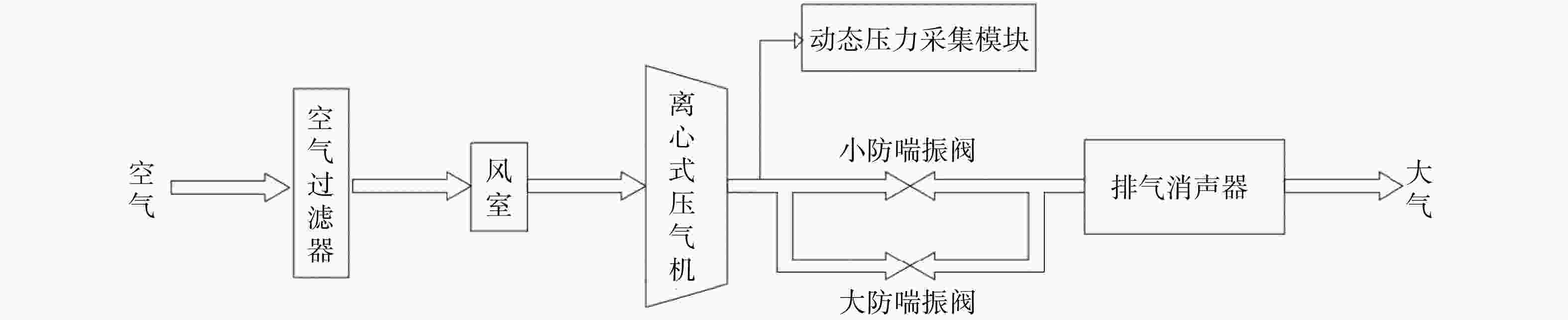
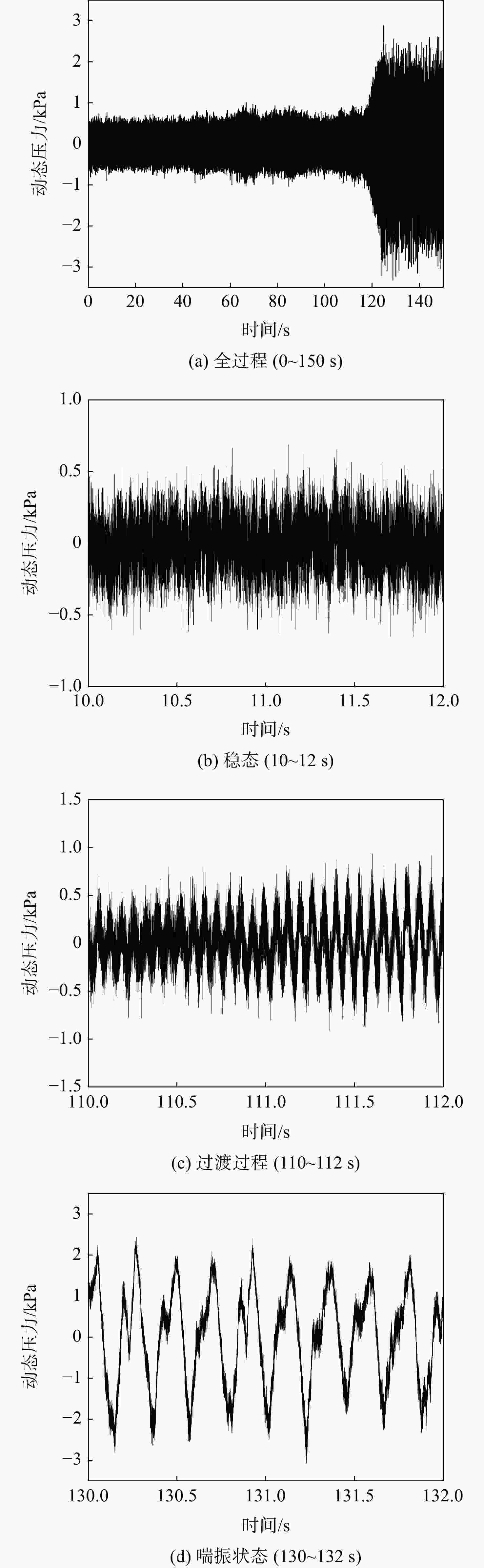
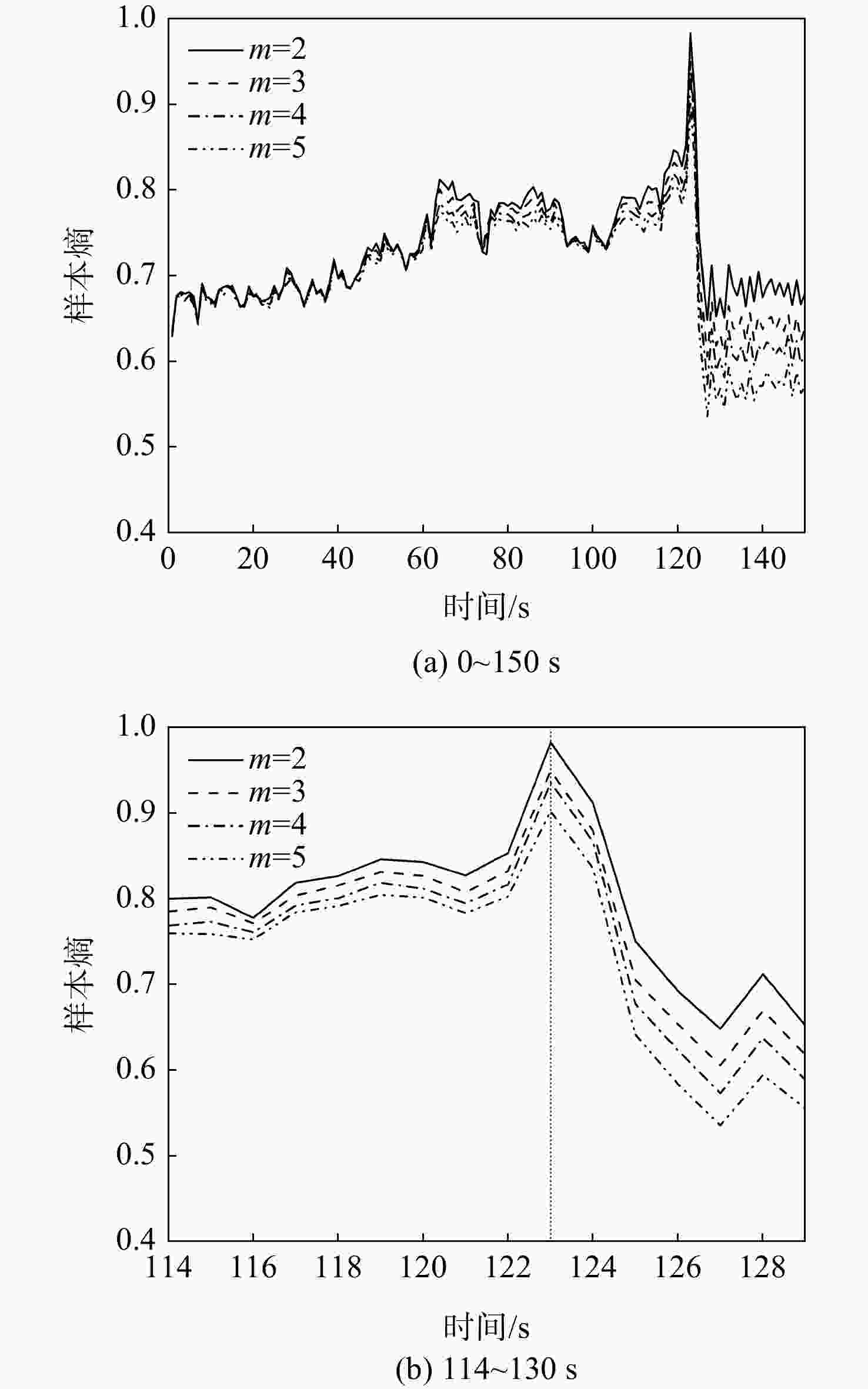
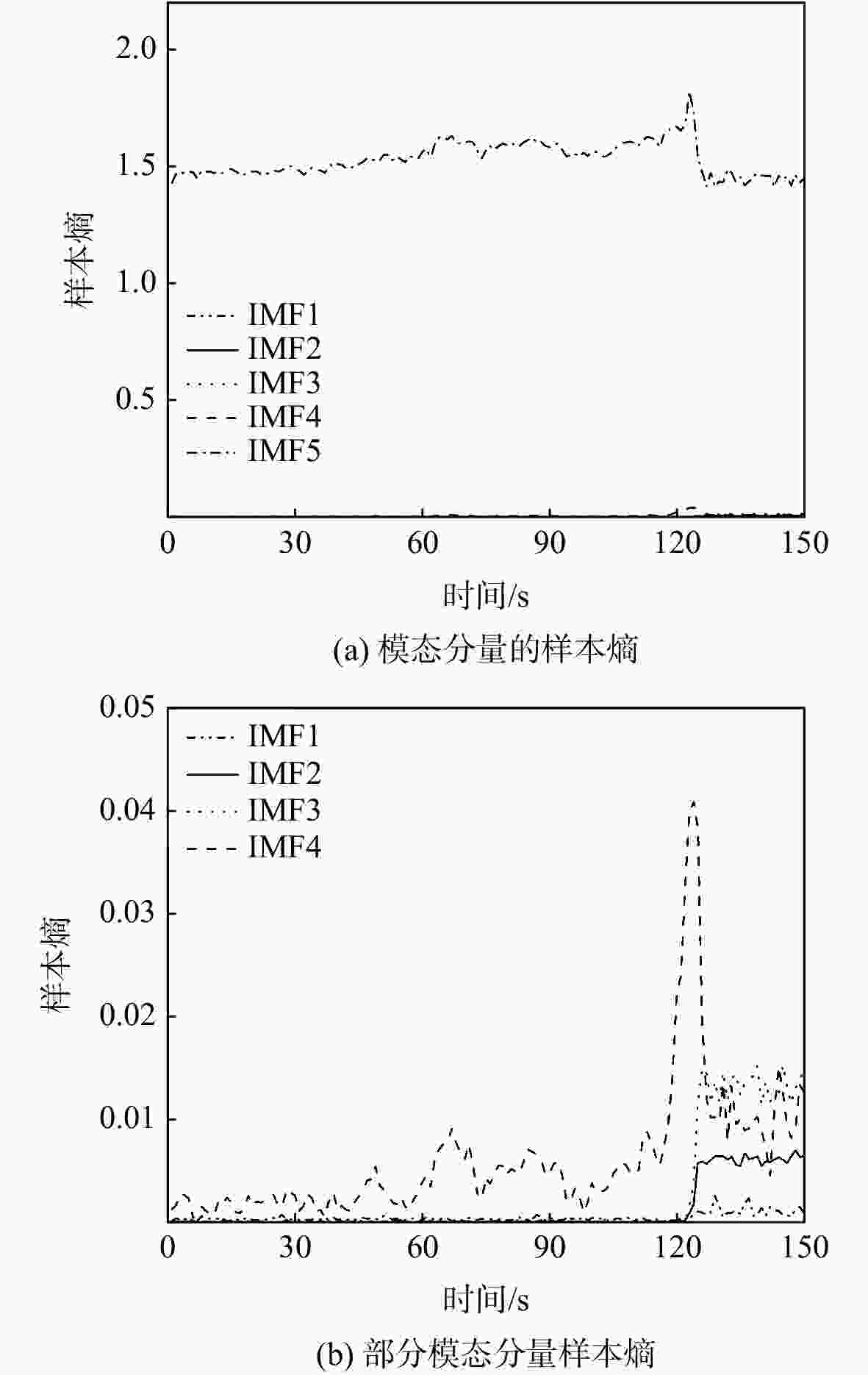
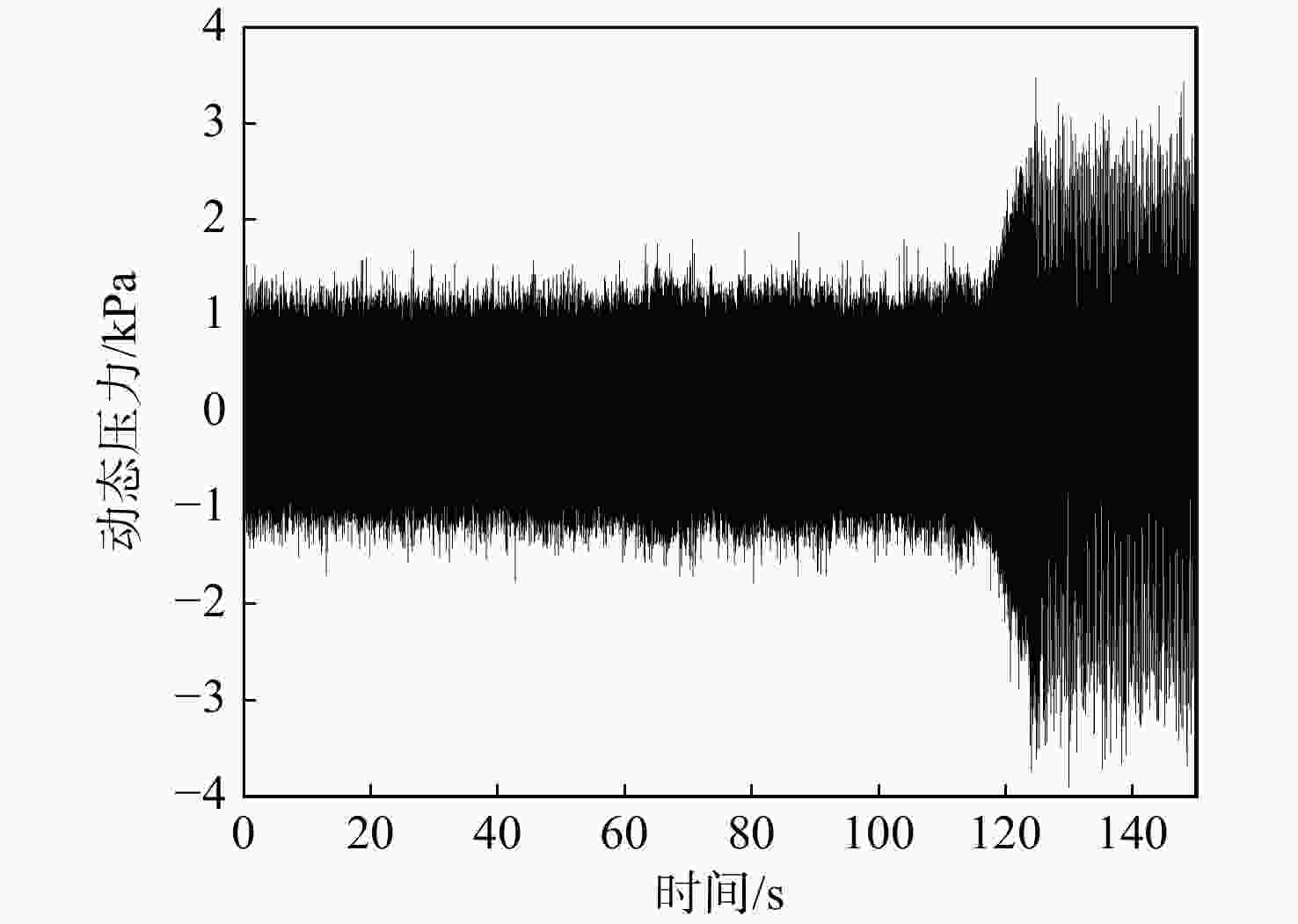
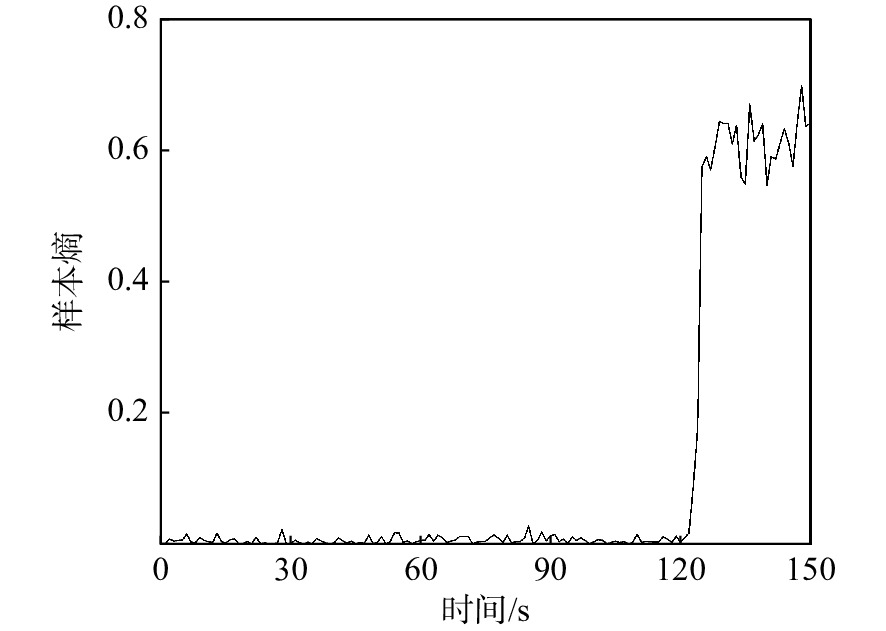
以800 kW离心压气机从稳定状态经过过渡过程进入喘振状态时段的出口动态压力为研究对象，采用经验小波变换并结合样本熵特征，分析了系统在不同工况下的复杂特性。首先，在分析系统动态压力波形特征的基础上，采用经验小波变换并结合皮尔逊相关系数进行信号的提取。其次，研究了提取信号的样本熵与系统工作状态变化的关联关系，并讨论了经验小波的分解层数和样本熵的维数对分析结果的影响。最后，通过将白噪声加入原始信号以验证该方法的抗干扰性能。研究结果显示：当系统由稳态进入喘振状态时，系统出口动态压力的样本熵表现出明显的突变特性，其值由0突变至0.7左右。从系统参数的选择角度，样本熵维数的变化对系统特征的分析影响较小。并且，采用该方法抗干扰性能较好。
- 离心压气机 /
- 喘振 /
- 动态压力 /
- 经验小波变换 /
- 样本熵
Abstract:
Taking the dynamic outlet pressure of the 800 kW centrifugal compressor during the period of transition from steady state to surge state as the research object, the empirical wavelet transform combined with sample entropy characteristics was used to analyze the complex characteristics of the system under different working conditions. First, on the basis of analyzing the characteristics of the dynamic pressure waveform of the system, the empirical wavelet transform combined with the Pearson correlation coefficient was used to extract the signal. Second, the relationship between the sample entropy of the extracted signal and the change of the system working state was analyzed to discuss the influence of the decomposition layer of the empirical wavelet and the dimension of the sample entropy on the analysis result. Finally, white noise was added to the original signal to verify the anti-interference performance of the method. The research results showed that when the system entered the surge state from the steady state, the sample entropy of the system outlet dynamic pressure showed an obviously sudden change characteristics, and its value changed from 0 to about 0.7. From the perspective of the selection of system parameters, the change of sample entropy dimension had little effect on the analysis of system characteristics. In addition, this method had better anti-interference performance.
- centrifugal compressor /
- surge /
- dynamic pressure /
- empirical wavelet transform /
- sample entropy

HTML

图 1 EWT分解图

Figure 1. EWT spectrum segmentation diagram

下载: 全尺寸图片幻灯片

图 2 采集系统

Figure 2. Acquisition system

下载: 全尺寸图片幻灯片

图 3 离心压气机出口动态压力波形

Figure 3. Dynamic pressure waveform at outlet of centrifugal compressor

下载: 全尺寸图片幻灯片

图 4 动态压力的频谱图

Figure 4. Spectrogram of dynamic pressure

下载: 全尺寸图片幻灯片

图 5 出口处样本熵

Figure 5. Sample entropy at exit

下载: 全尺寸图片幻灯片

图 6 出口动态压力的EWT分解

Figure 6. EWT decomposition of outlet dynamic pressure

下载: 全尺寸图片幻灯片

图 7 模态分量的样本熵（L=5，m=2）

Figure 7. Sample entropy of modal component （L=5, m=2）

下载: 全尺寸图片幻灯片

图 8 IMF2的样本熵（L=5）

Figure 8. Sample entropy of IMF2 （L=5）

下载: 全尺寸图片幻灯片

图 9 含有白噪声的出口动态压力

Figure 9. Dynamic pressure at exit with white noise

下载: 全尺寸图片幻灯片

图 10 EWT分解结果

Figure 10. EWT decomposition results

下载: 全尺寸图片幻灯片

图 11 引入比例系数后IMF2的样本熵（L=5）

Figure 11. Sample entropy of IMF2 with scale coefficient （L=5）

下载: 全尺寸图片幻灯片

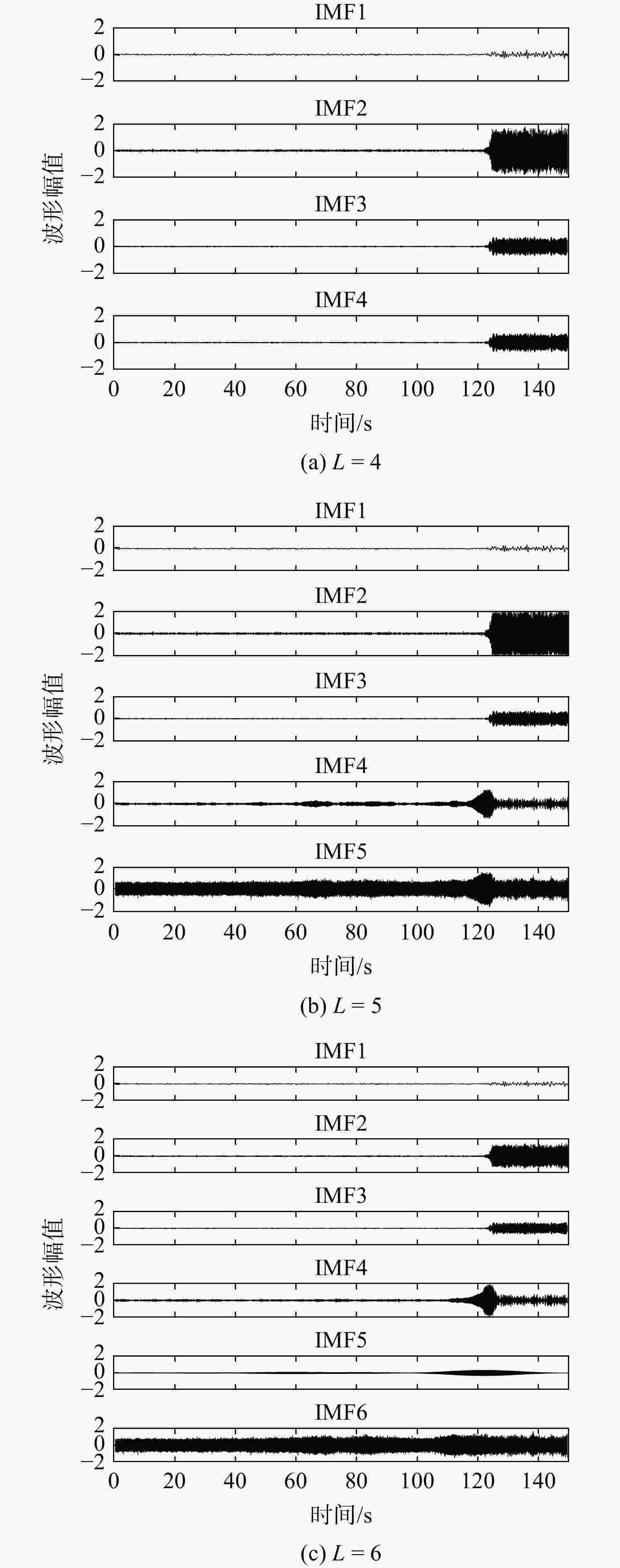
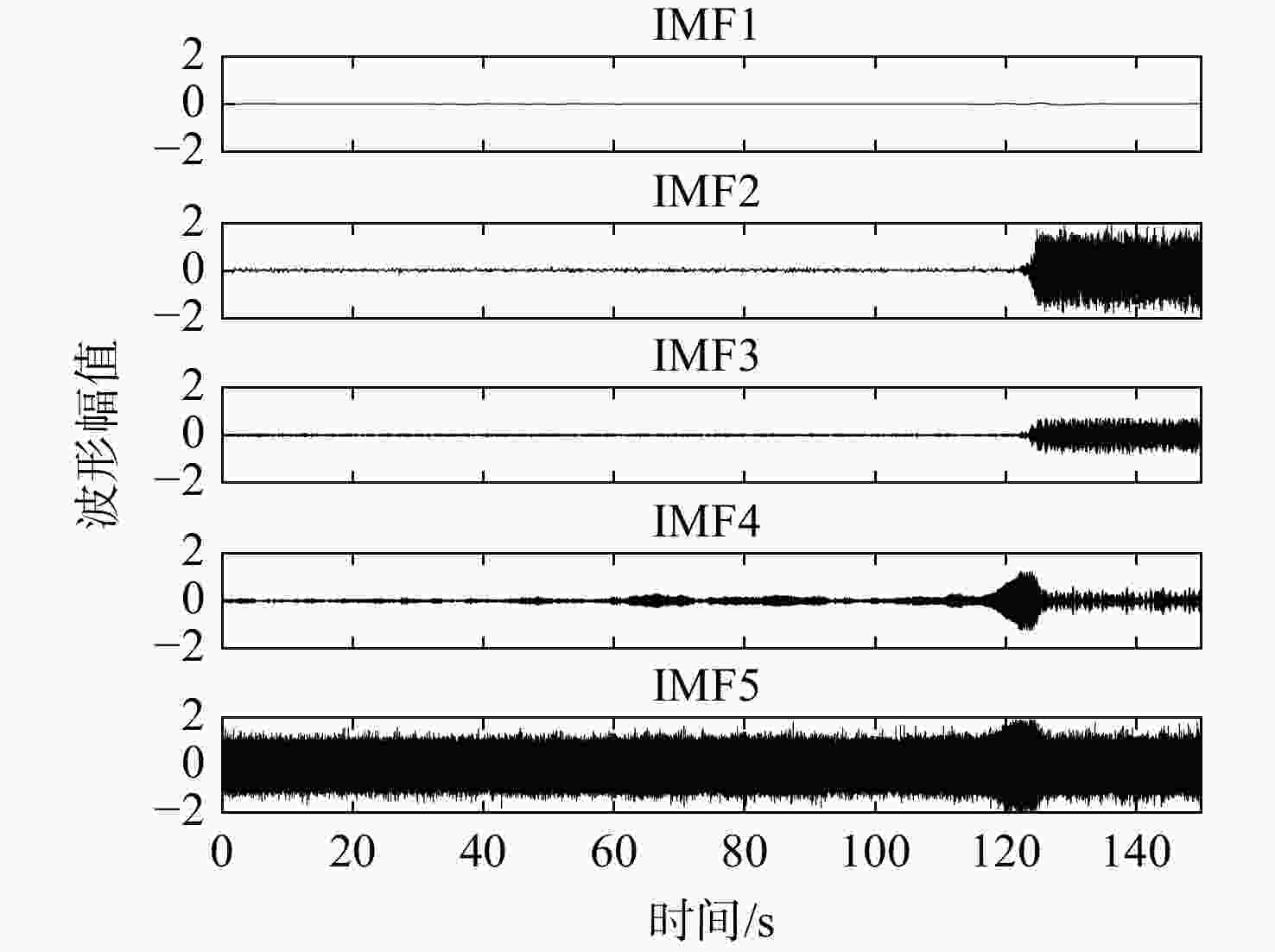
表 1 各个模态分量与原始信号的相关性

Table 1. Correlation of each modal component with original signal

分层相关系数
IMF1 IMF2 IMF3 IMF4 IMF5 IMF6

L=4 0.097 0.812 0.302 0.5191
L=5 0.096 0.812 0.302 0.410 0.485
L=6 0.096 0.796 0.300 0.3218 0.165 0.382

下载: 导出CSV

表 2 含有白噪声的模态分量与原始信号的相关性

Table 2. Correlation between white noise-containing modal components and original signal

分层相关系数
IMF1 IMF2 IMF3 IMF4 IMF5

L=5 0.0135 0.799 0.314 0.4078 0.2880

下载: 导出CSV

参考文献(20)

[1]	GUNADAL S M,GOVARDHAN M. Improvement in stable operating range of a centrifugal compressor with leaned diffuser vanes[J]. Journal of Mechanical Science and Technology,2019,33(11): 5261-5269. doi: 10.1007/s12206-019-1017-3
[2]	刘云龙,吕文浩,鲁悦. 离心式压缩机喘振分析及预防措施[J]. 内燃机与配件,2020(20): 121-122. doi: 10.3969/j.issn.1674-957X.2020.20.054 LIU Yunlong,LÜ Wenhao,LU Yue,et al. Analysis and preventive measures of centrifugal compressor surge[J]. Internal Combustion Engine and Parts,2020(20): 121-122. (in Chinese) doi: 10.3969/j.issn.1674-957X.2020.20.054
[3]	刘雁,高宽,何浩,等. 基于多重分形的离心压缩机出口动态压力非线性特征研究及其在喘振识别中的应用[J]. 振动与冲击,2021,40(1): 205-211, 214. doi: 10.13465/j.cnki.jvs.2021.01.027 LIU Yan,GAO Kuan,HE Hao,et al. Nonlinear characteristics of centrifugal compressor outlet dynamic pressure based on multifractal and their application in surge identification[J]. Journal of Vibration and Shock,2021,40(1): 205-211, 214. (in Chinese) doi: 10.13465/j.cnki.jvs.2021.01.027
[4]	VEPA R,CATTANI C. Modelling and quasilinear control of compressor surge and rotating stall vibrations[J]. Mathematical Problems in Engineering,2010,2010: 314172.1-314172.21.
[5]	LI Zhiping,ZHANG Peng,PAN Tianyu,et al. Hysteresis behaviors of compressor rotating stall with cusp catastrophic model[J]. Chinese Journal of Aeronautics,2018,31(5): 1075-1084. doi: 10.1016/j.cja.2018.02.010
[6]	GBANAIBOLOU J,JIRI P,SURESH S,et al. Influence of fouling on compressor dynamics: experimental and modeling approach[J]. Journal of Engineering for Gas Turbines and Power,2018,140(3): 032603.1-032603.7.
[7]	王聪,文彬鹤,司文杰,等. 轴流压气机旋转失速建模与检测: Ⅰ 基于确定学习理论与高阶Moore-Greitzer模型的研究[J]. 自动化学报,2014,40(7): 1265-1277. WANG Cong,WEN Binhe,SI Wenjie,et al. Modeling and detection of rotation stall in axial flow compressors: Part Ⅰ investigation on high-order M-G models via deterministic learning[J]. Acta Automatica Sinica,2014,40(7): 1265-1277. (in Chinese)
[8]	刘雁,陈党民,柳黎光,等. 离心式压缩机出口动态压力的单重分形特征研究[J]. 西北工业大学学报,2013,31(1): 60-66. doi: 10.3969/j.issn.1000-2758.2013.01.012 LIU Yan,CHEN Dangmin,LIU Liguang,et al. Exploring monofractal characteristics of dynamic pressure at exit of centrifugal compressor[J]. Journal of Northwestern Polytechnical University,2013,31(1): 60-66. (in Chinese) doi: 10.3969/j.issn.1000-2758.2013.01.012
[9]	刘雁,何浩,肖军. 离心式压气机出口动态压力的关联维数特征分析[J]. 航空动力学报,2021,36(2): 300-309. doi: 10.13224/j.cnki.jasp.2021.02.008 LIU Yan,HE Hao,XIAO Jun. Correlation dimension characteristics analysis of dynamic pressure at centrifugal compressor outlet[J]. Journal of Aerospace Power,2021,36(2): 300-309. (in Chinese) doi: 10.13224/j.cnki.jasp.2021.02.008
[10]	HE Xiao,ZHENG Xinqian. Roles and mechanisms of casing treatment on different scales of flow instability in high pressure ratio centrifugal compressors[J]. Aerospace Science and Technology,2019,84: 734-746. doi: 10.1016/j.ast.2018.10.015
[11]	SUN Zhenzhong,ZOU Wangzhi,ZHENG Xinqian. Instability detection of centrifugal compressors by means of acoustic measurements[J]. Aerospace Science and Technology,2018,82/83: 628-635. doi: 10.1016/j.ast.2018.09.006
[12]	刘晨,张文平,曹贻鹏,等. 模化设计对离心压气机气动噪声的影响[J]. 航空动力学报,2019,34(2): 486-494. doi: 10.13224/j.cnki.jasp.2019.02.025 LIU Chen,ZHANG Wenping,CAO Yipeng,et al. Effects of modeling design on centrifugal compressor aerodynamic noise[J]. Journal of Aerospace Power,2019,34(2): 486-494. (in Chinese) doi: 10.13224/j.cnki.jasp.2019.02.025
[13]	YAN Ruqiang,GAO R X. Approximate entropy as a diagnostic tool for machine health monitoring[J]. Mechanical Systems and Signal Processing,2006,21(2): 824-839.
[14]	PINCUS S M. Approximate entropy as a complexity measure[J]. Chaos,1995,5(1): 110-117. doi: 10.1063/1.166092
[15]	GILLES J. Empirical wavelet transform[J]. IEEE Transactions on Signal Processing,2013,61(16): 3999-4010. doi: 10.1109/TSP.2013.2265222
[16]	OUNG Q W, MUTHUSAMY H, BASAH S N, et al. Empirical wavelet transform based features for classification of Parkinson’s disease severity[J]. Journal of Medical Systems, 2018, 42(2): 292-308.
[17]	KEDADOUCHE M,THOMAS M,TAHAN A. A comparative study between empirical wavelet transforms and empirical mode decomposition methods: application to bearing defect diagnosis[J]. Mechanical Systems and Signal Processing,2016,81: 88-107. doi: 10.1016/j.ymssp.2016.02.049
[18]	DAUBECHIES I. Ten lectures on wavelets[M]. Philadelphia, US: Siam Publications, 1992.
[19]	RICHMAN J S,MOORMAN J R. Physiological time-series analysis using approximate entropy and sample entropy[J]. American Journal of Physiology-Heart and Circulatory Physiology,2000,278(6): 2039-2049. doi: 10.1152/ajpheart.2000.278.6.H2039
[20]	ZHANG T,YANG Z,COOTE J H. Cross-sample entropy statistic as a measure of complexity and regularity of renal sympathetic nerve activity in the rat[J]. Experimental Physiology,2007,92(4): 659-669. doi: 10.1113/expphysiol.2007.037150