航空发动机初步设计阶段榫接结构前置判别方法

董少静; 方宇凡; 胡文通; 申秀丽

doi:10.13224/j.cnki.jasp.20220356

航空发动机初步设计阶段榫接结构前置判别方法

doi: 10.13224/j.cnki.jasp.20220356

董少静^{1, 2,},
方宇凡^{1, 2,},
胡文通³,
申秀丽^{1, 2,*, ,}

1.
北京航空航天大学能源与动力工程学院，北京 100191
2.
北京航空航天大学航空发动机结构强度北京市重点实验室，北京 100191
3.
中国兵器工业集团导航与控制技术研究所，北京 100089

详细信息

作者简介:
董少静（1986-），女，副研究员、博士生导师，博士，主要从事航空发动机热端部件结构、材料及工艺方面的研究

通讯作者:
申秀丽（1967-），女，研究员、博士生导师，博士，主要从事航空发动机热端部件结构强度及多学科优化、陶瓷基复合材料在发动机热端部件的应用、高温合金多尺度力学分析等方面的研究。E-mail：shxl606@buaa.edu.cn

中图分类号: V232.3
计量
- 文章访问数: 159
- HTML浏览量: 50
- PDF量: 60
- 被引次数: 0
出版历程
- 收稿日期: 2022-05-21
- 网络出版日期: 2022-09-30

Prejudgment method of tenon structure in aero-engine preliminary design stage

DONG Shaojing^{1, 2
,},
FANG Yufan^{1, 2
,},
HU Wentong³,
SHEN Xiuli^{1, 2,*
, ,}

1.
School of Energy and Power Engineering， Beihang University，Beijing 100191，China
2.
Beijing Key Laboratory of Aero-Engine Structure and Strength， Beihang University，Beijing 100191，China
3.
Navigation and Control Technology Research Institute，China North Industries Group Corporation Limited，Beijing 100089，China

摘要

摘要:
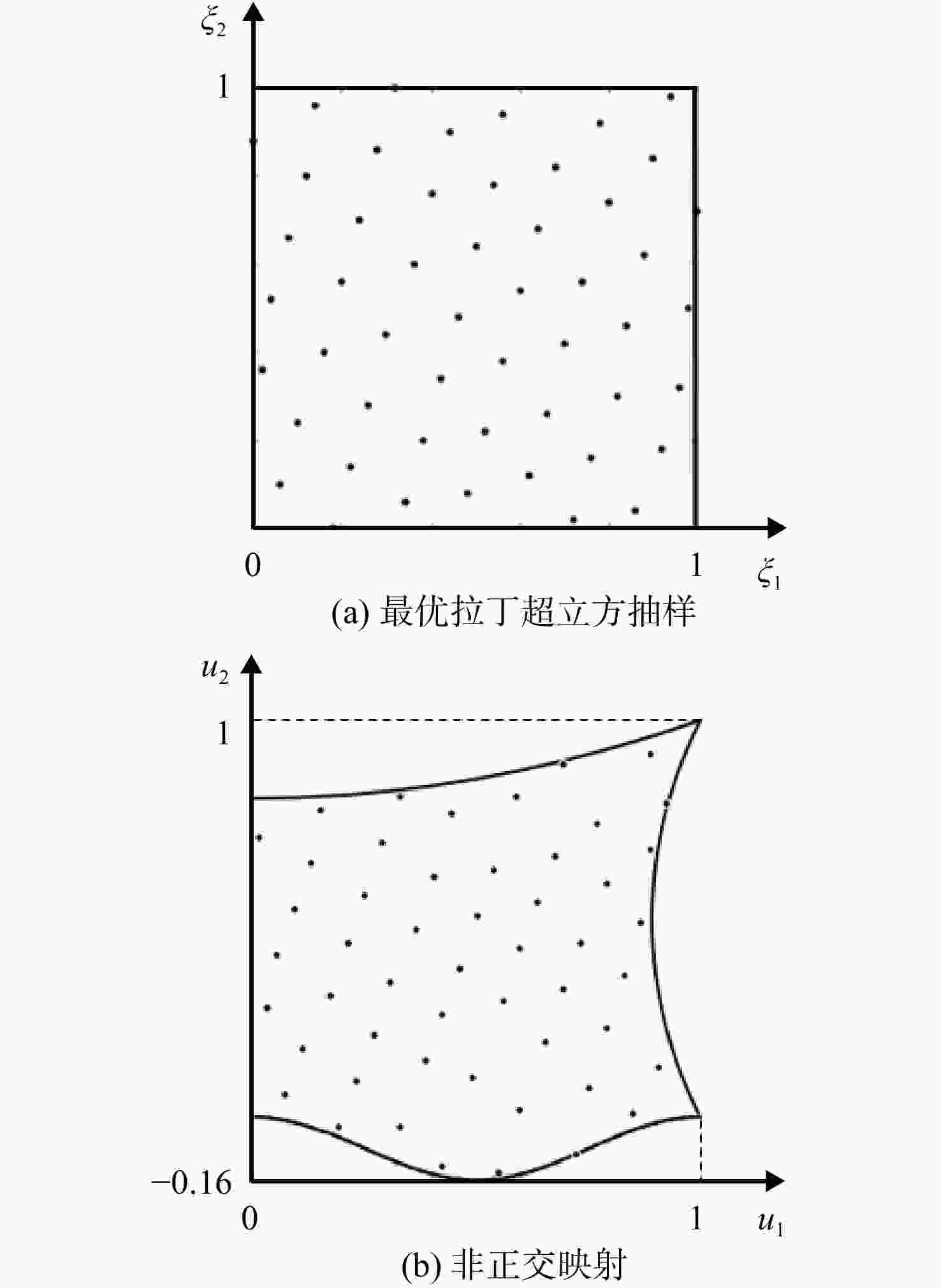
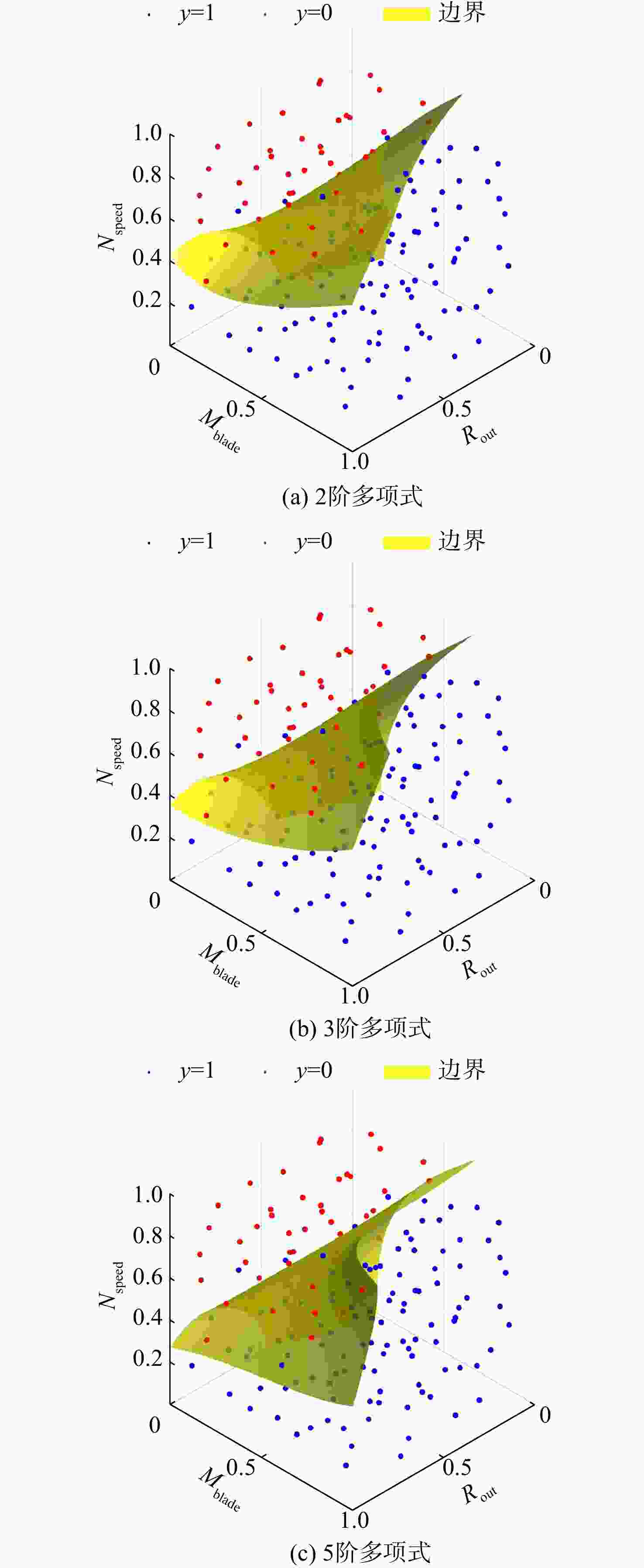
为适应自约束参数化建模方法所导致的非正交参数取值范围，提出了将传统正交设计空间的抽样点映射到非正交空间的映射方法。构建了基于机器学习逻辑回归的可行域边界识别方法，对样本空间响应是否满足相关准则进行判断。将此方法应用于某高压涡轮二齿和三齿榫接结构，发现某发动机初步设计方案会导致在详细设计阶段无法获得满足设计要求的榫接结构，需将榫接结构参数前置至初步设计阶段，与上级参数共同设计，防止其在详细设计阶段成为设计难点。通过边界识别方法发现，转速降低为15 575 r/min或轮盘外径降低为303 mm时可以设计出二齿榫接结构；转速降低为15 584 r/min或轮盘外径降低为301 mm时可以设计出三齿榫接结构。该方法可以作为发动机初步设计阶段各学科之间的一个迭代反馈信息，在发动机其他细节结构设计上具有推广性。
- 初步设计阶段 /
- 颠覆性设计 /
- 榫接结构 /
- 可行域边界识别 /
- 前置参数设计
Abstract:
In order to adapt to the range of non-orthogonal parameters caused by the self-constrained parametric modeling method, a mapping method was proposed to map the sampling points of the traditional orthogonal design space to the non-orthogonal space. A feasible domain boundary identification method based on machine learning logistic regression was constructed to judge the compliance of the sample space response with relevant criteria. This method was applied to a high pressure turbine two-/ three-tooth tenon structure, finding that an engine preliminary design scheme may fail to meet the design requirements in the detailed design phase of tenon structure, and tenon structure parameters may be advanced to the preliminary design stage, together with the superior parameter design, to prevent the design difficulties in the detailed design stage. Through the boundary identification method, it was found that when the speed was reduced to 15 575 r /min or the outer diameter of the wheel was reduced to 303 mm, the two-tooth tenon structure can be designed. When the speed was reduced to 15 584 r /min or the outer diameter of the wheel was reduced to 301 mm, the three-tooth tenon structure can be designed. This method can be used as an iterative feedback information among various disciplines in the initial engine design stage. The proposed method can be generalized to other details of the engine structure design.
- preliminary design stage /
- disruptive design /
- tenon structure /
- feasible region boundary recognition method /
- pre-parameter design

HTML

图 1 非正交边界示意图

Figure 1. Diagram of nonorthogonal boundaries

下载: 全尺寸图片幻灯片

图 2 两因子51水平非正交映射效果

Figure 2. Two factors 51 level non-orthogonal mapping effect

下载: 全尺寸图片幻灯片

图 3 两因子逻辑回归样本

Figure 3. Two factors logistic regression sample

下载: 全尺寸图片幻灯片

图 4 两因子不同阶次多项式逻辑回归边界识别结果

Figure 4. Boundary identification results of two factor with different order polynomial logistic regression

下载: 全尺寸图片幻灯片

图 5 涡轮盘子午面模型

Figure 5. Model of meridional plane of turbine disc

下载: 全尺寸图片幻灯片

图 6 榫接结构参数化模型^[18]

Figure 6. Parametric model of tenon structure^[18]

下载: 全尺寸图片幻灯片

图 7 初始二齿榫接结构

Figure 7. Initial two-tooth tenon structure

下载: 全尺寸图片幻灯片

图 8 建模层级划分

Figure 8. Modeling hierarchy

下载: 全尺寸图片幻灯片

图 9 榫头第N齿底部圆角预留空间

Figure 9. Leave space at the bottom corner of the N_th tooth of the tenon

下载: 全尺寸图片幻灯片

图 10 榫头齿顶圆角半径几何约束

Figure 10. Geometric constraints on the radius of the fillet at the top of tenon teeth

下载: 全尺寸图片幻灯片

图 11 榫头齿高几何约束

Figure 11. Geometric constraints on tenon tooth height

下载: 全尺寸图片幻灯片

图 12 榫槽底部双圆弧几何约束

Figure 12. Double circular arc geometric constraints at the bottom of the groove

下载: 全尺寸图片幻灯片

图 13 三齿榫接结构周向应力分布

Figure 13. Circumferential stress distribution of three-tooth tenon structure

下载: 全尺寸图片幻灯片

图 14 三齿榫接结构径向应力分布

Figure 14. Radial stress distribution of three-tooth tenon structure

下载: 全尺寸图片幻灯片

图 15 优化前后三齿榫接结构

Figure 15. Optimization of the front and rear three-tooth tenon structure

下载: 全尺寸图片幻灯片

图 16 二齿榫接结构二维图

Figure 16. Two-dimensional drawings of two-tooth tenon structure

下载: 全尺寸图片幻灯片

图 17 二齿榫接结构三维图

Figure 17. Three-dimensional drawings of two-tooth tenon structure

下载: 全尺寸图片幻灯片

图 18 高压涡轮三齿榫接结构样本响应分布

Figure 18. Sample response distribution of three-tooth tenon structure of high pressure turbine

下载: 全尺寸图片幻灯片

图 19 高压涡轮二齿榫接结构样本响应分布

Figure 19. Sample response distribution of two-tooth tenon structure of high pressure turbine

下载: 全尺寸图片幻灯片

图 20 三齿榫接结构逻辑回归边界识别结果

Figure 20. Boundary identification results of logistic regression for three-tooth tenon structure

下载: 全尺寸图片幻灯片

图 21 二齿榫接结构逻辑回归边界识别结果

Figure 21. Boundary identification results of logistic regression for two-tooth tenon structure

下载: 全尺寸图片幻灯片

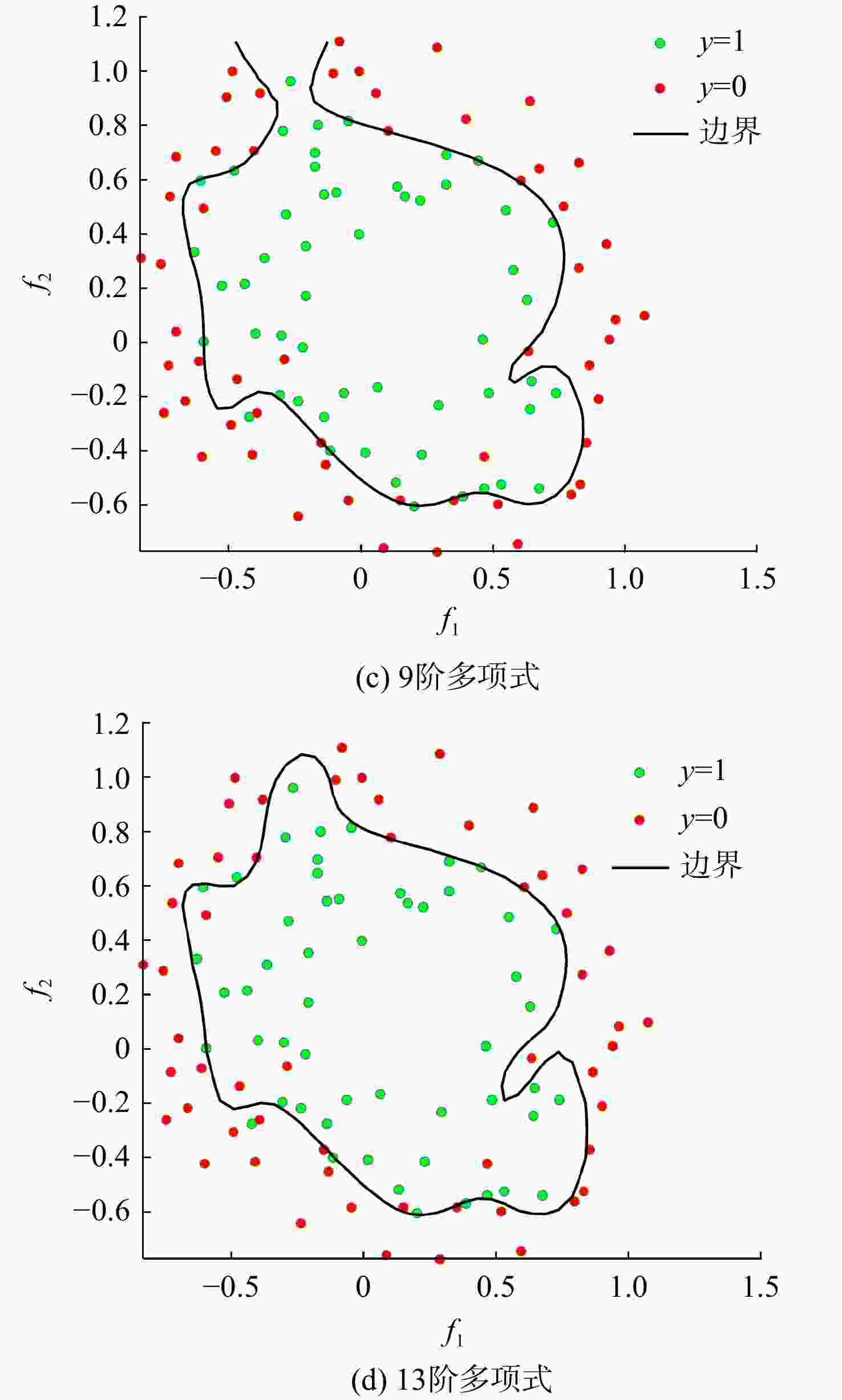
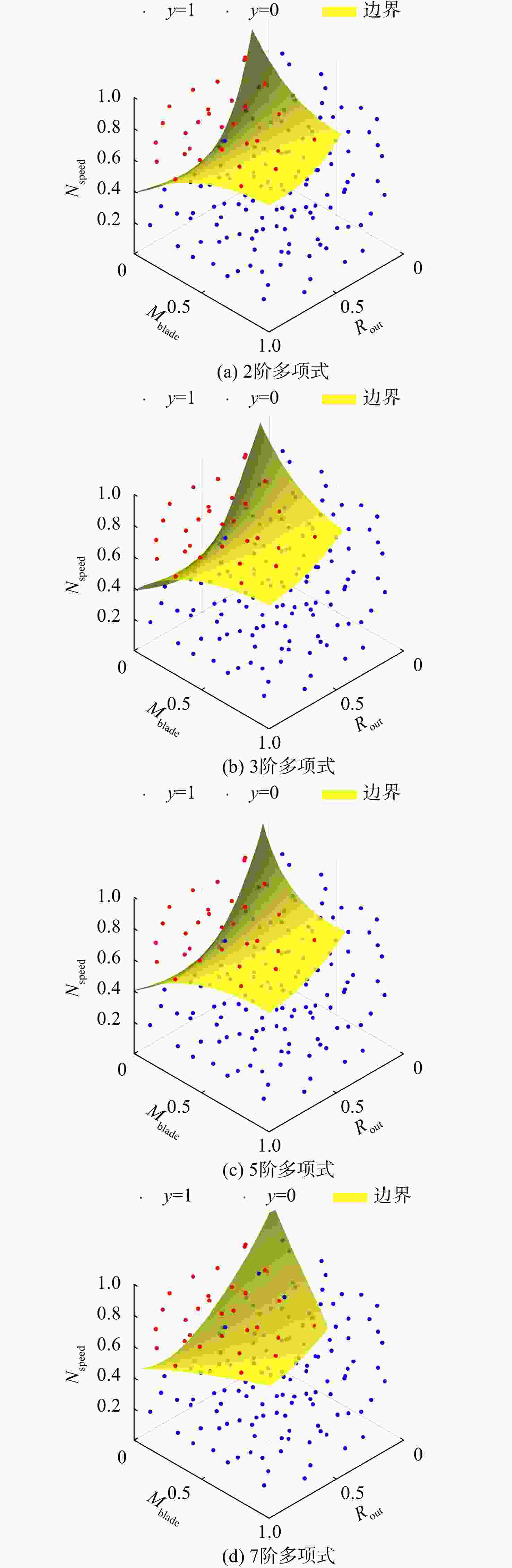
表 1 两因子不同阶次多项式逻辑回归拟合精度

Table 1. Two factors of different order polynomial logistic regression fitting accuracy

多项式阶次	多项式系数个数	回归拟合精度/%
2	6	86.11
3	10	86.11
4	15	85.19
5	21	88.89
6	28	88.89
7	36	90.74
8	45	91.67
9	55	91.67
10	66	91.67
11	78	92.59
12	91	90.74
13	105	91.67

下载: 导出CSV

表 2 高压涡轮榫接结构关键技术判别上级参数取值范围

Table 2. Value range of superior parameters for key technology discrimination of high pressure turbine tenon structure

上级参数	下限值	上限值
轮盘外径/mm	280	320
叶片质量矩/（g·m）	35	80
转速/（rad/s）	1400	1700

下载: 导出CSV

表 3 高压涡轮榫接结构关键技术前置判别参数

Table 3. Prejudgment parameters of key technologies of high pressure turbine tenon structure

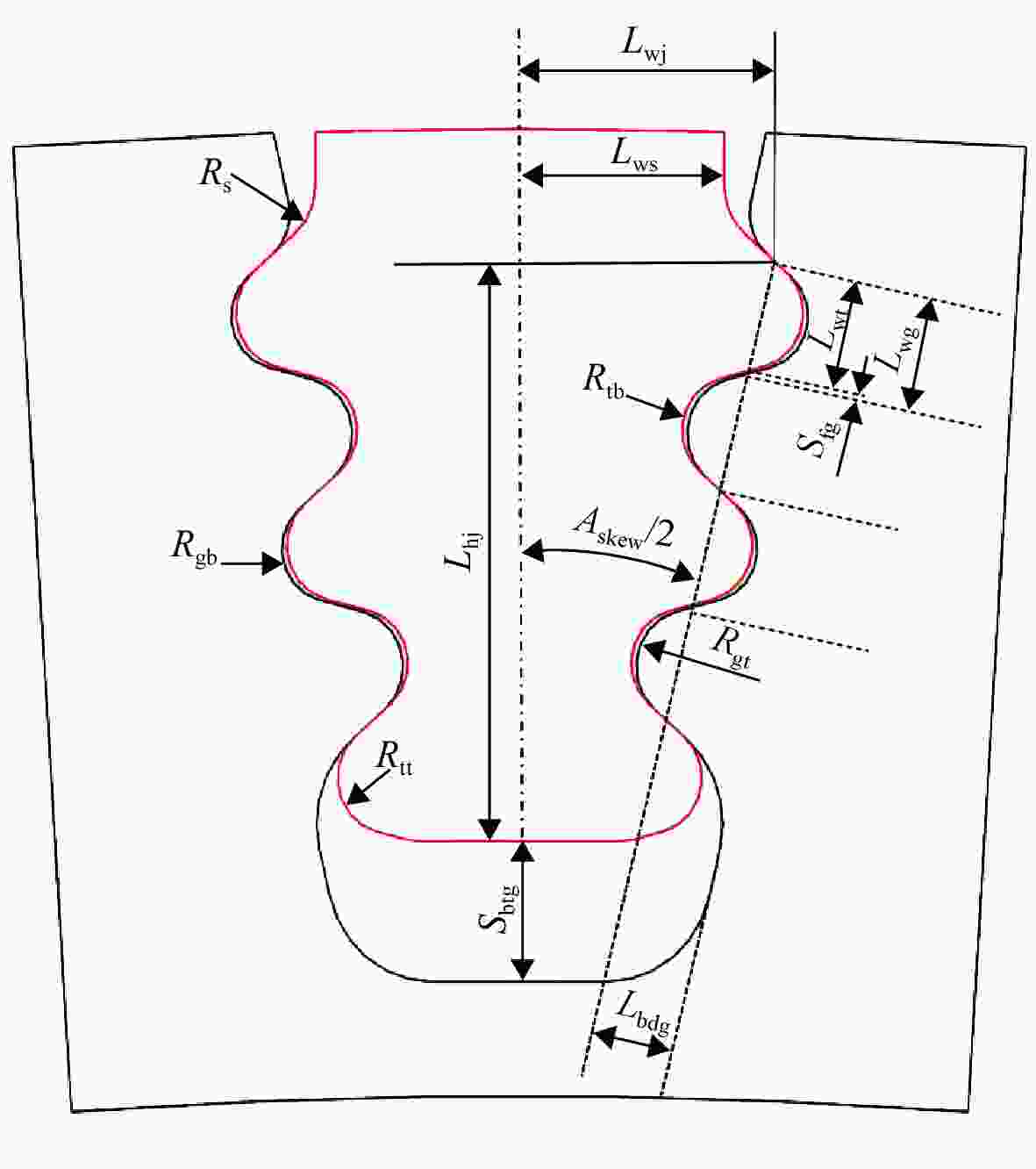
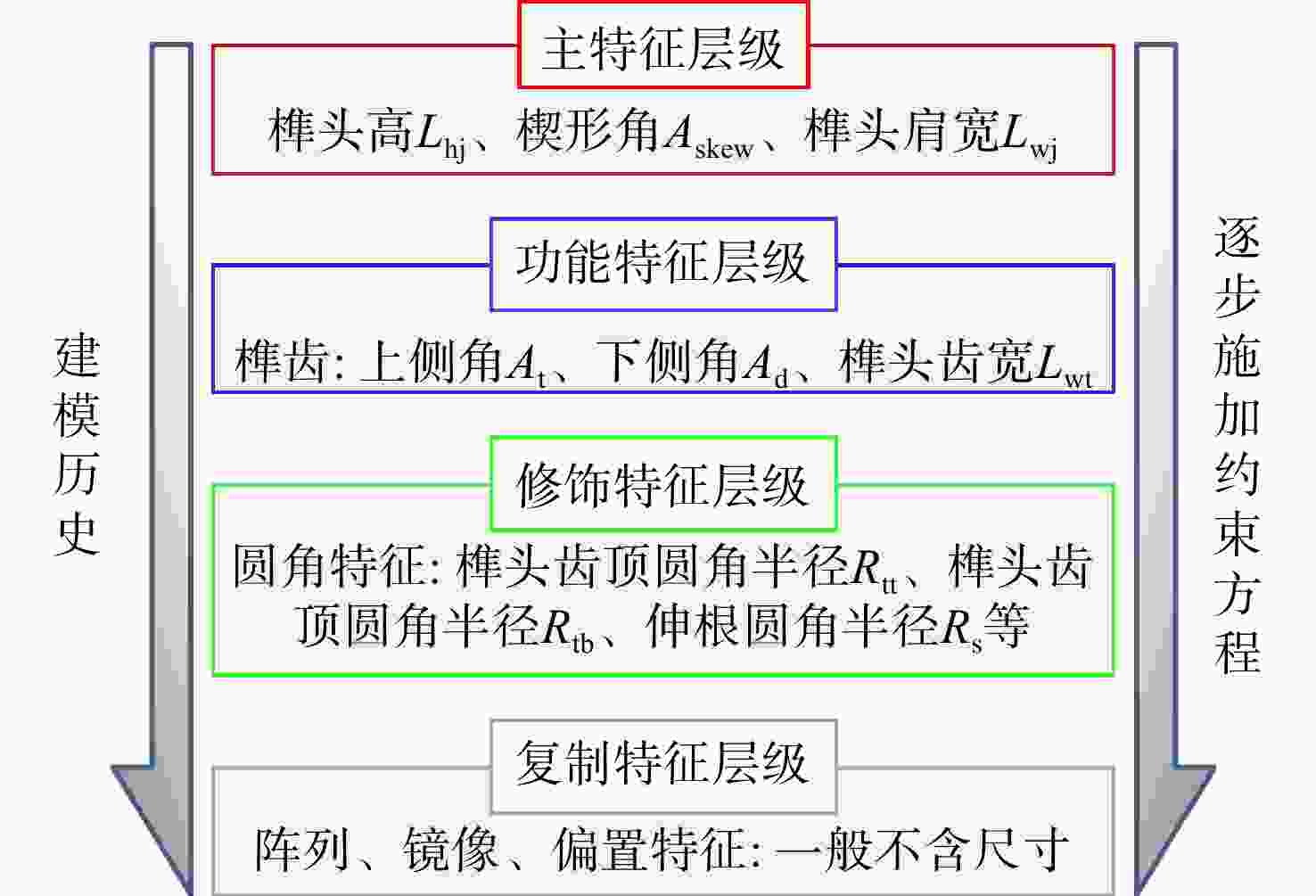
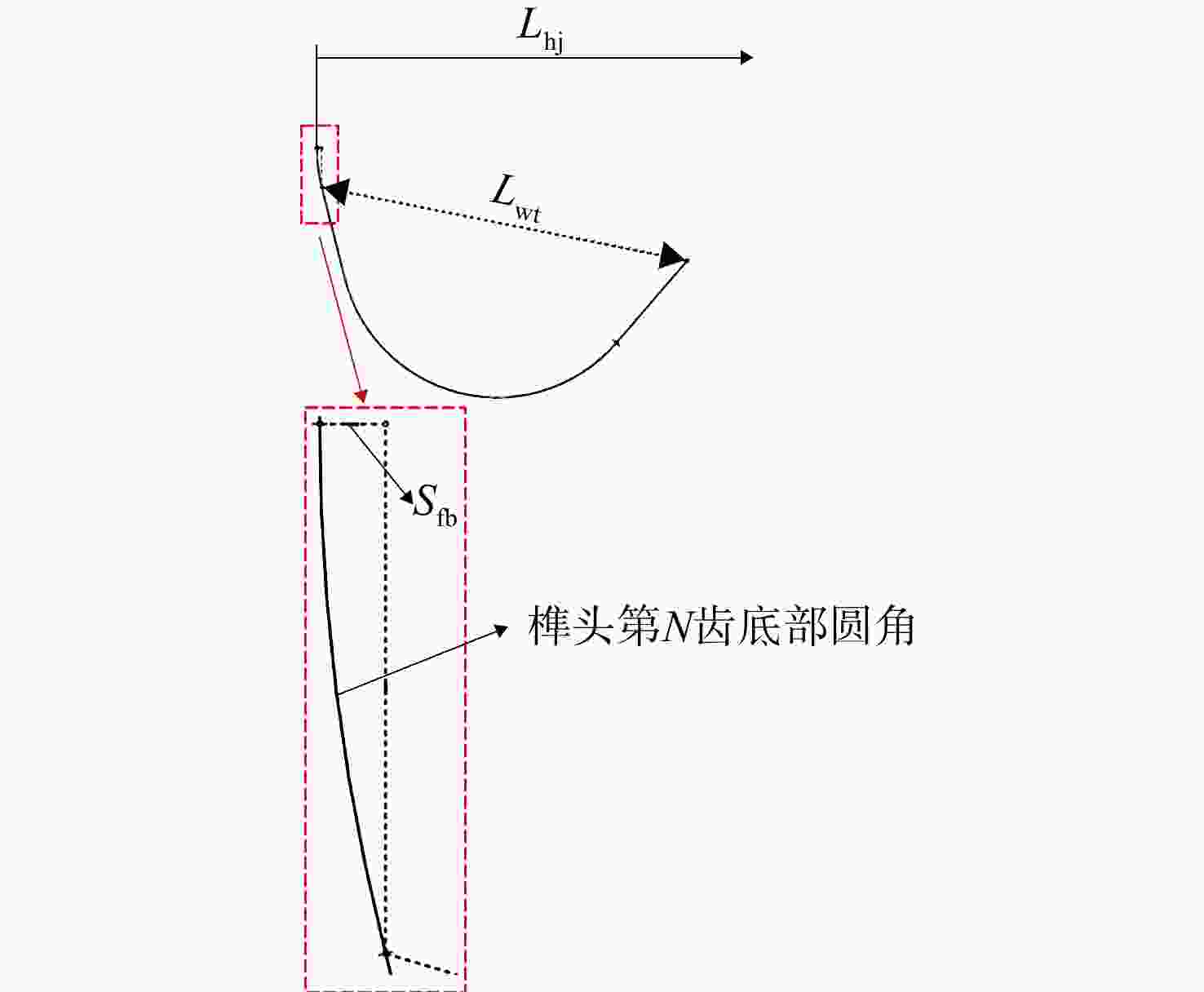
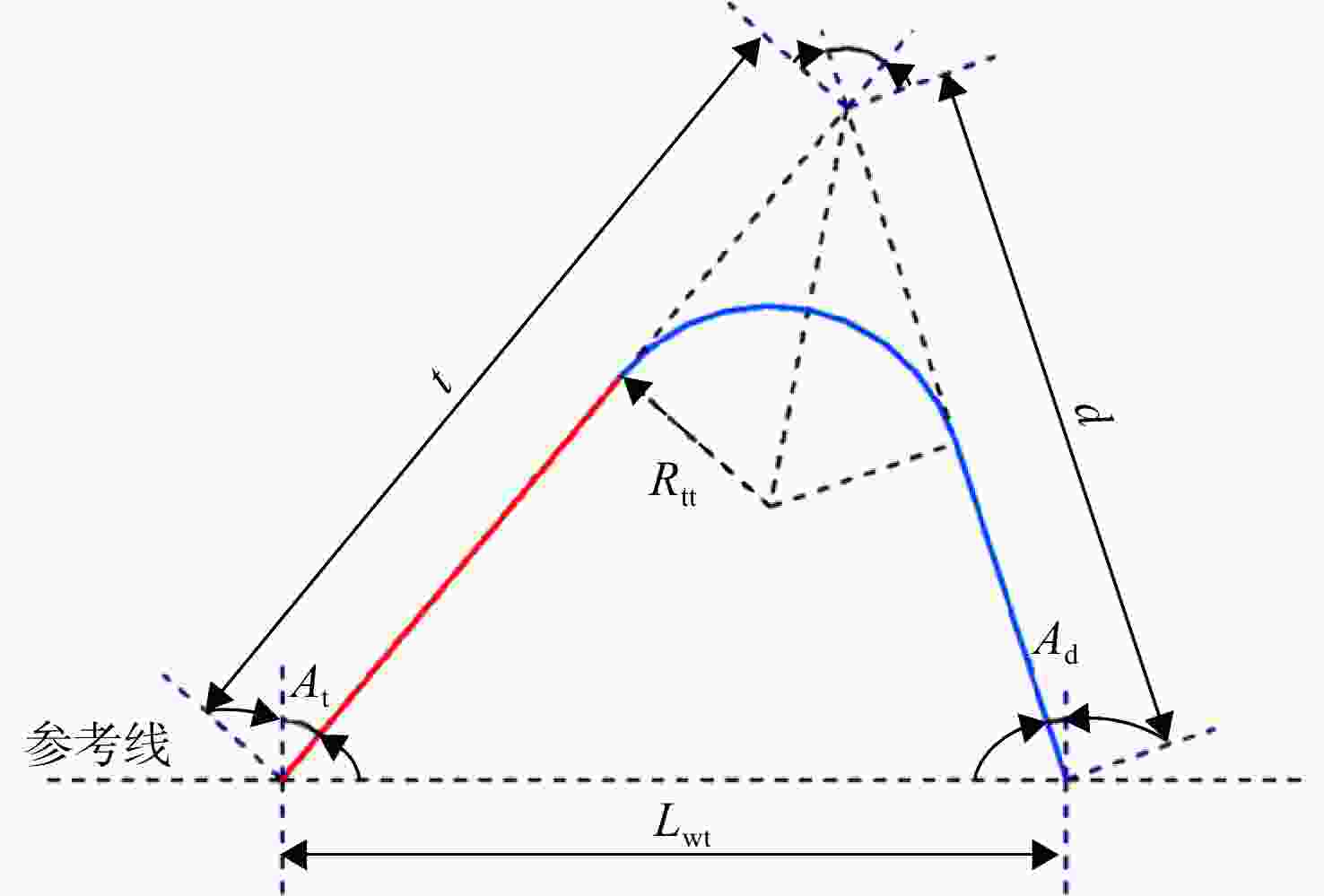
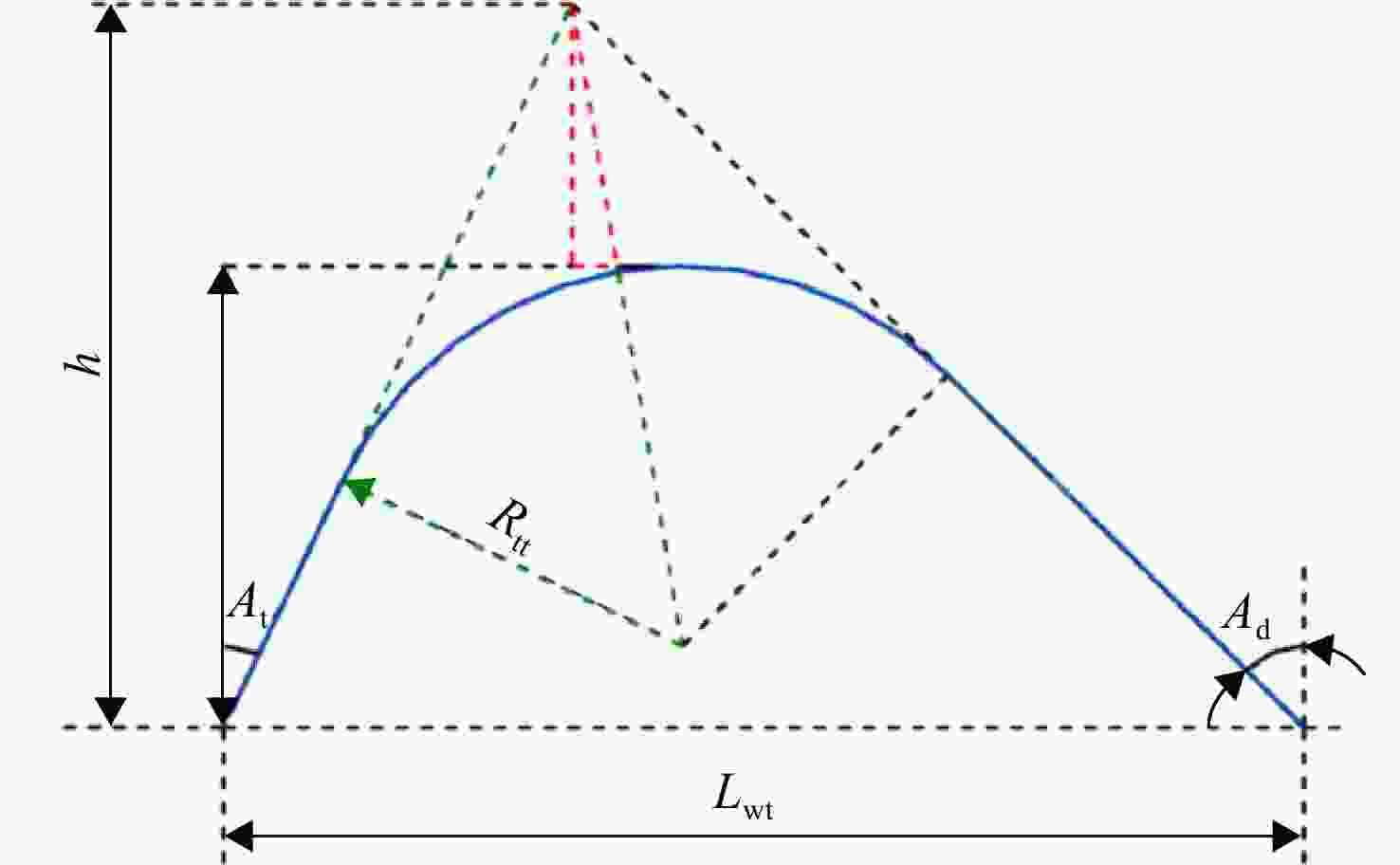
上级参数	下级参数
上级参数	独立参数	半独立参数	非独立参数
轮盘外径	榫头高L_hj	榫头齿顶圆角半径R_tt	榫头齿宽L_wt
叶片质量矩	榫头颈宽L_wj	榫槽齿底圆角半径R_gb	榫头齿高L_ht
转速	楔形角A_skew	榫槽齿顶圆角半径R_gt	榫槽齿宽L_wg
	上侧角A_t	榫头齿底圆角半径R_tb
	下侧角A_d	伸根圆角半径R_s
	榫头榫槽齿宽间隙S_fg	榫槽第N齿齿深L_bdg
	榫头榫槽底部间隙S_btg	榫槽第N齿上圆弧半径R_bgb
	榫头底预留圆角空间S_fb	榫槽第N齿下圆弧半径R_tgb
	伸根颈宽L_ws
	盘心等厚区轴向厚度H₁

下载: 导出CSV

表 4 涡轮盘安全储备系数

Table 4. Safety reserve factor of turbine disc

参数	安全储备系数
参数	弹性极限	破坏极限
子午面平均周向应力	1.33	1.57
子午面沿半径圆环最大平均径向应力	1.33	1.57
盘心最大周向应力	0.90
辐板最大单点径向应力	0.90

下载: 导出CSV

表 5 仿真成本

Table 5. Cost of simulation

分析类型	总时长/min	单步平均耗时/s	实际平均耗时/s
轴对称分析	1438	52.52	52.52
三维分析	7043	130.30	124.99

下载: 导出CSV

表 6 不同阶次逻辑回归拟合精度

Table 6. Fitting accuracy of different order logistic regression

多项式阶次	多项式系数个数	三齿拟合精度/%	二齿拟合精度/%
2	10	97.5155	94.4099
3	20	98.1366	96.2733
4	35	97.5155	93.7888
5	56	98.1366	93.1677
6	84	96.8944	93.7888
7	120	96.8944	95.6521

下载: 导出CSV

表 7 三齿榫接结构逻辑回归边界函数

Table 7. Logistic regression boundary function of three-tooth tenon structure

特征项	1	x	z	y	x²	xz	z²
特征项系数	3.8953	−10.2121	9.5142	30.1708	6.5452	−14.3047	−1.9825

特征项	xy	yz	y²	x³	x²z	xz²	z³
特征项系数	7.9126	3.3575	2.2901	9.8839	−10.3288	−22.8682	−8.2799

特征项	x²y	xyz	yz²	xy²	y²z	y³
特征项系数	4.0047	−10.6481	−4.7281	−5.8400	−8.3353	−1.5545
注：表中x 表示轮盘外径，y 表示叶片质量矩， z 表示轮盘转速，下同。

下载: 导出CSV

表 8 二齿榫接结构逻辑回归边界函数

Table 8. Logistic regression boundary function of two-tooth tenon structure

特征项	1	x	z	y	x²	xz	z²
特征项系数	−6.5744	12.8410	2.1666	40.9794	11.3447	−15.6261	−19.3266

特征项	xy	yz	y²	x³	x²z	xz²	z³
特征项系数	−23.9871	−21.7655	8.1815	−11.6826	−6.5967	26.6870	6.0329

特征项	x²y	xyz	yz²	xy²	y²z	y³
特征项系数	−7.8526	−6.2959	−0.3774	−1.8543	−0.3100	5.3692

下载: 导出CSV

表 9 三齿榫接结构关键设计判别结果

Table 9. Jugment results of key design of three-tooth tenon structure

上级参数	实际初值	归一化初值	$\theta （{\boldsymbol{X}}）$	$g （ {\theta （{\boldsymbol{X}}）} ）$
轮盘外径	308 mm	0.7000	−4.17	0.02
叶片质量矩	60 g·m	0.5556
轮盘转速	15800 r/min	0.8500

下载: 导出CSV

表 10 二齿榫接结构关键设计判别结果

Table 10. Jugment results of key design of two-tooth tenon structure

上级参数	实际初值	归一化初值	$\theta （{\boldsymbol{X}}）$	$g （ {\theta （{\boldsymbol{X}}）} ）$
轮盘外径	308 mm	0.7000	−1.25	0.22
叶片质量矩	60 g·m	0.5556
轮盘转速	15800 r/min	0.8500

下载: 导出CSV

参考文献(21)

[1]	尹泽勇,米栋,吴立强,等. 航空发动机多学科设计优化技术研究[J]. 中国工程科学,2007,9(6): 1-10. doi: 10.3969/j.issn.1009-1742.2007.06.001 YIN Zeyong,MI Dong,WU Liqiang,et al. Research on multidisciplinary design optimization technology of aero engine[J]. Strategic Study of Chinese Academy of Engineering,2007,9(6): 1-10. (in Chinese) doi: 10.3969/j.issn.1009-1742.2007.06.001
[2]	SAMPATH R, PLYBON R, MEYERS C, et al. High fidelity system simulation of aerospace vehicles using NPSS[R]. AIAA-2004-371, 2004.
[3]	《航空发动机设计手册》总编委会. 航空发动机设计手册: 第5册涡喷及涡扇发动机总体[M]. 北京: 航空工业出版社, 2001.
[4]	黄鲁成,成雨,吴菲菲,等. 关于颠覆性技术识别框架的探索[J]. 科学学研究,2015,33(5): 654-664. doi: 10.3969/j.issn.1003-2053.2015.05.003 HUANG Lucheng,CHENG Yu,WU Feifei,et al. Exploration of a framework for identifying disruptive technologies[J]. Research of Science of Science,2015,33(5): 654-664. (in Chinese) doi: 10.3969/j.issn.1003-2053.2015.05.003
[5]	WIMMER M A,PEREIRA G V,RONZHYN A,et al. Transforming government by leveraging disruptive technologies: identification of research and training needs[J]. The Journal of Democracy and Open Government,2020,12(1): 87-114. doi: 10.29379/jedem.v12i1.594
[6]	SHIBATA N,KAJIKAWA Y,TAKEDA Y,et al. Detecting emerging research fronts in regenerative medicine by the citation network analysis of scientific publications[J]. Technological Forecasting and Social Change,2011,78(2): 274-282. doi: 10.1016/j.techfore.2010.07.006
[7]	MOMENI A,ROST K. Identification and monitoring of possible disruptive technologies by patent-development paths and topic modeling[J]. Technological Forecasting and Social Change,2016,104: 16-29. doi: 10.1016/j.techfore.2015.12.003
[8]	BUCHANAN B, CORKEN R. A toolkit for the systematic analysis of patent data to assess a potentially disruptive technology[R]. London: Intellectual Property Office, 2010.
[9]	GIUNTA A, WOJTKIEWICZ S, ELDRED M. Overview of modern design of experiments methods for computational simulations[R]. AIAA 2003-649, 2003.
[10]	YETURU K. Machine learning algorithms, applications, and practices in data science[J]. Handbook of Statistics,2020,43: 81-206.
[11]	JURAFSKY D, MATIN J H. Speech and language processing[M]. 2nd ed. Upper Saddle River, US: Prentice Hall, 2008.
[12]	THOMPSON J F. A general three-dimensional elliptic grid generation system on a composite block structure[J]. Computer Methods in Applied Mechanics and Engineering,1987,64(1/2/3): 377-411.
[13]	李卫平. 计算流体力学[M]. 武汉: 华中科技大学出版社, 2004.
[14]	GOLDMAN A,KAO Y C. Numerical solution to a two-dimensional conduction problem using rectangular and cylindrical body-fitted coordinate systems[J]. Journal of Heat Transfer,1981,103(4): 753-758. doi: 10.1115/1.3244537
[15]	程俊霞. 椭圆型网格生成方法及其应用[D]. 南京: 南京理工大学, 2002. CHENG Junxia. Elliptic mesh generation method and its application[D]. Nanjing: Nanjing University of Science and Technology, 2022. (in Chinese)
[16]	华冬英, 李祥贵. 微分方程的数值解法与程序实现[M]. 北京: 电子工业出版社, 2016.
[17]	周志华. 机器学习[M]. 北京: 清华大学出版社, 2016.
[18]	胡文通. 细节结构在航空发动机初步设计阶段前置优化技术研究[D]. 北京: 北京航空航天大学, 2019. HU Wentong. Research on pre-optimization technology of detail structure in aeroengine preliminary design stage[D]. Beijing: Beihang University, 2019. (in Chinese)
[19]	赵海. 涡轮榫头/榫槽结构设计方法研究[D]. 南京: 南京航空航天大学, 2005. ZHAO Hai. Study on design method of tenon/mortise structure for turbine[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2005. (in Chinese)
[20]	RR公司. Spey MK202发动机应力标准(EGD-3)[M]. 北京: 国际航空编辑部, 1979.
[21]	LU S,LI L. Twin-web structure optimization design for heavy duty turbine disk based for aero-engine[J]. Journal of Propulsion Technology,2011,32(5): 631-636.