直升机尾传动轴是直升机传动系统的重要组成部分，承担着将主减速器的动力传递至尾减速器的作用。当传动轴以临界速度运行时，由于其存在加工误差，非常微小的不平衡量都能使传动轴发生很大地振动。如果不施加额外的阻尼，传动轴的过大振动将使支承或轴本身发生破坏失效。为了避免临界转速的共振影响，直升机尾传动轴通常采用亚临界设计方案，即传动轴工作转速在1阶临界转速之下。通过降低传动轴的工作转速或提高传动轴的临界速度，可以实现传动轴的亚临界设计。但当传动轴以较低的转速运行，要传递同样的功率则需要增加扭矩，这就需要传动轴要有较高的承载能力，使得轴本身的结构更重、更大。而通过增加临界转速实现亚临界设计也存在一定的弊端。例如缩小轴跨长度，选择大直径的刚性短轴并设置较多支承，能够提高传动轴的临界转速，但这也导致传动系统结构复杂且质量较大。随着直升机技术的发展，高速、绿色、安全成为未来直升机的发展趋势^[1]。亚临界设计由于上述的种种限制越来越不能满足直升机发展需求。而在超临界设计中，传动轴的工作转速在1阶临界转速甚至2阶临界转速之上^[2]。由于运行转速高，传递扭矩小，因此传动轴可以选用细长轴，这样就减小了支承数量，同时较少的轴段也意味着传动系统具有较高的可靠性。因此超临界设计方案越来越得到研究人员的注意，已经成为直升机尾传动轴设计的发展趋势，波音AH-64、阿古斯塔AB129、欧直EC175等先进直升机均采用超临界设计方案^[3]。

采用超临界设计则需要对传动轴跨临界转速进行减振。应用在直升机尾传动轴上的减振器主要有两种：一种是黏弹性减振器，安装在支承处，一种是限幅减振器，安装在轴跨中间。黏弹性减振器利用黏弹性材料本身的特性为系统提供阻尼，其应用范围十分广泛^[4-6]。针对黏弹性减振器，国内外已经做了很多的研究^[7-11]，理论相对成熟。但由于超临界轴的跨度较大，黏弹性减振器的减振作用有限。限幅减振器是针对直升机超临界尾轴的跨临界减振设计的一种专用减振器，只在传动轴跨临界转速时发挥减振作用，而在传动轴正常工作时不发挥作用。

国内外对于限幅减振器已经进行了一些研究。Özaydın^[12]针对限幅减振器内部的碰摩环与摩擦片之间的干摩擦力，建立了3种不同的摩擦力模型。通过谐波平衡法得到了3种不同摩擦力模型下的系统非线性方程解，对临界干摩擦力、间隙及分布位置对系统的振幅及共振频率的影响进行了分析，但其并未考虑传动轴的涡动，忽略了传动轴与碰摩环之间的切向碰摩力。Dżygadło和Perkowski^[13-15]考虑传动轴与减振器之间的非线性碰摩，建立了系统的动力学模型，主要分析了临界干摩擦力及间隙对减振效果的影响。其研究结果表明，在大临界干摩擦力、小间隙的情况下减振效率较高，但可能导致传动轴进入混沌。Huang等人^[16]考虑限幅减振器内部碰摩环与底座之间的间隙，首次建立了带有双间隙的限幅减振器与传动轴系统动力学模型，其研究发现增大临界干摩擦力能提高减振效率，但会使系统更加不稳定。在其之后的研究中^[17]，忽略了碰摩环的运动，将减振器视为固定定子，主要分析了复合材料轴内部阻尼及陀螺力矩对相位差及系统稳定性的影响。

以上的研究主要针对传动轴过1阶临界转速的减振过程进行建模。相较于工作在1阶临界转速之上，传动轴工作在2阶临界转速之上时具有更高的功率密度及可靠性，但也意味着减振器需对转轴跨1阶及2阶过程均能实现高效减振。考虑到过1阶临界转速时转轴中部振幅最大，因此当转轴只过1阶临界转速时，可将减振器直接安装在轴跨中间，即可实现对转轴的高效减振。而当转轴跨2阶临界转速时，由于其2阶振型与1阶不同，若要同时实现对两个过临界过程的高效减振，则需进一步对减振器的安装位置进行研究。为了研究清楚限幅减振器安装位置对减振效果的影响，本文采用有限元方法建立传动轴与限幅减振器系统的动力学模型，通过数值计算得到了系统动力学响应。首先对系统典型过临界过程的响应结果进行分析，在此基础上进一步研究了限幅减振器的安装位置对传动轴振动特性的影响。

1.   带限幅减振器的单跨轴系动力学模型

1.1   物理模型

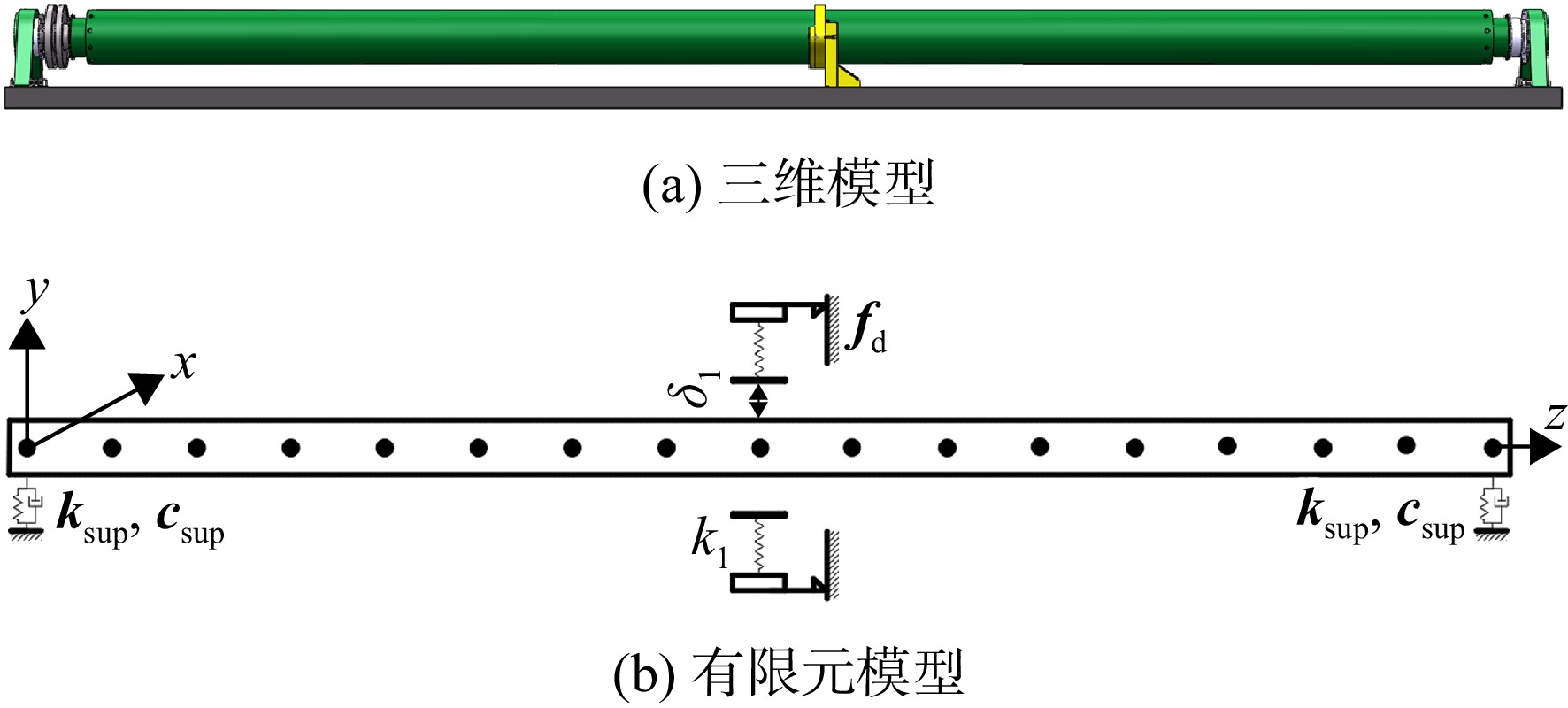
图1为限幅减振器的结构示意图。限幅减振器主要由碰摩环、摩擦片、预紧弹簧等组成。传动轴安装在碰摩环内部，与碰摩环之间存在间隙${\delta _1}$，碰摩环通过螺栓安装在底座上同时两侧装有摩擦片，通过预紧弹簧向摩擦片施加预紧力。在预紧力的作用下，摩擦片与碰摩环之间产生干摩擦力，当碰摩环克服临界干摩擦力将产生滑动。

图  1  限幅减振器结构示意图

Figure  1.  Structure diagram of the dry friction damper

下载: 全尺寸图片 幻灯片

对于本文所研究的传动轴跨临界振动过程，单跨转子轴即可比较完整的呈现转子动力学行为特征。因此本文基于带限幅减振器的单跨轴进行动力学建模，说明限幅减振器与传动轴系统的非线性动力学特性。

1.2   系统动力学方程

系统模型如图2所示。将空心传动轴划分为16个轴段，共17个节点。采用Timoshenko梁单元模型建立传动轴模型，每个节点有4个自由度，分别为x、y方向平移自由度及绕x、y方向的转动自由度。转轴的单元刚度矩阵、单元质量矩阵、单元阻尼矩阵及单元陀螺矩阵分别表示为${{\boldsymbol{k}}_{\text{e}}}$、${{\boldsymbol{m}}_{\text{e}}}$、${{\boldsymbol{c}}_{\text{e}}}$及${{\boldsymbol{g}}_{\text{e}}}$^[18]，其中阻尼矩阵采用瑞利阻尼。设两端轴承径向支承刚度为${k_{\sup }}$，支承阻尼为${c_{\sup }}$。支承节点刚度矩阵为${{\boldsymbol{k}}_{\sup }} = {\text{diag}}\left[ {{k_{\sup }},{k_{\sup }},0,0} \right]$，支承单元阻尼矩阵为${{\boldsymbol{c}}_{\sup }} = {\text{diag}}\left[ {{c_{\sup }},{c_{\sup }},0,0} \right]$。图2中k₁为法向碰摩刚度。

图  2  带限幅减振器的单跨轴系模型

Figure  2.  Model of the signal shaft system with a dry friction damper

下载: 全尺寸图片 幻灯片

将各单元矩阵组装，得到传动轴整体刚度矩阵${{\boldsymbol{k}}_{\text{s}}}$，整体质量矩阵${{\boldsymbol{m}}_{\text{s}}}$，整体阻尼矩阵${{\boldsymbol{c}}_{\text{s}}}$，整体陀螺矩阵${{\boldsymbol{g}}_{\text{s}}}$。

设传动轴的位移矩阵为${{\boldsymbol{q}}_{\text{s}}}$，得到传动轴的动力学方程：

式中f为传动轴所受外界激励力，主要包括偏心激励及碰摩力，${{\boldsymbol{\dot q}}_{\text{s}}}$、${{\boldsymbol{\ddot q}}_{\text{s}}}$分别为${{\boldsymbol{q}}_{\text{s}}}$对时间的1阶导数及2阶导数，$\omega$为传动轴转速。设作用在某一节点上的偏心激励力为${{\boldsymbol{f}}_{\text{e}}}$，其表达式为

式中${m_{\text{n}}}e$为不平衡量，e为偏心距离，${m_{\text{n}}}$为等效质量，$\theta$为传动轴转角，$\dot \theta$、$\ddot \theta$分别为$\theta$对时间的1阶导数及2阶导数。

传动轴与限幅减振器之间产生碰摩力，设碰摩环受到的碰摩力为${{\boldsymbol{f}}_1}$，则传动轴节点受到的碰摩力为

式中${f_{1x}}$、${f_{1y}}$为碰摩力${{\boldsymbol{f}}_1}$在x、y方向上的分量。

仅考虑碰摩环在x、y方向上的平移自由度，则碰摩环的位移矩阵${{\boldsymbol{q}}_{\text{r}}} = {\left[ {{x_{\text{r}}},{y_{{\mathrm{r}}} }} \right]^{\text{T}}}$。设碰摩环的质量为${m_{\text{r}}}$，则碰摩环的质量矩阵为${{\boldsymbol{m}}_{\text{r}}} = {\text{diag}}\left[ {{m_{\text{r}}},{m_{\text{r}}}} \right]$。碰摩环受到碰摩力及干摩擦力的作用，设碰摩环与摩擦片之间的干摩擦力为${{\boldsymbol{f}}_{\text{d}}}$，则碰摩环的动力学方程为

式中${f_{{\text{d}}x}}$、${f_{{\text{d}}y}}$为干摩擦力${{\boldsymbol{f}}_{\text{d}}}$在x、y方向上的分量。

1.3   非线性力模型

在碰摩环几何中心所处的横截面上对传动轴与碰摩环进行受力分析，如图3所示。图中${O_1}$为转子几何中心，$C$为转子质心，e为偏心距离，${O_2}$为碰摩环几何中心，传动轴超越间隙${\delta _1}$与碰摩环发生碰摩，其中碰摩环受到的法向碰摩力为${f_{1{\text{n}}}}$，切向碰摩力为${f_{{\text{1t}}}}$，${\varphi _1}$为法向碰摩力与x轴的夹角。

图  3  非线性力模型

Figure  3.  Nonlinear force model

下载: 全尺寸图片 幻灯片

采用分段线性弹簧模型计算法向碰摩力^[19]，得到法向碰摩力的表达式为

式中$\varTheta （{\varepsilon _1}）$为Heaviside函数，其表达式为

其中${\varepsilon _1}$为传动轴与碰摩环之间在碰摩点处的侵入位移，${k_1}$为法向碰摩刚度。设安装限幅减振器处的传动轴节点横向振动位移为${x_{\text{s}}}$、${y_{\text{s}}}$，碰摩环的位移为${x_{\text{r}}}$、${y_{\text{r}}}$，则${\varepsilon _1}$的表达式为

切向碰摩力采用库伦摩擦模型，表达式为

式中${\mu _1}$为传动轴与碰摩环之间的切向碰摩摩擦因数，${v_{\text{1}}}$为传动轴与碰摩环之间在碰摩点的切向相对速度，其表达式为

式中${d_2}$为传动轴的外径，$\cos\; {\varphi _1}$、$\sin\; {\varphi _1}$可通过式（10）求得。

则${{\boldsymbol{f}}_1}$在x、y方向上的分量${f_{{\text{1}}x}}$、${f_{{\text{1}}y}}$的表达式为

碰摩环与摩擦片之间的干摩擦力采用库伦摩擦模型^[20]，表达式为

式中${v_{\text{r}}}$为碰摩环运动速度，${v_{\text{r}}} = { （{\dot x_{\text{r}}}^2 + {\dot y_{\text{r}}}^2） ^{1/2}}$，${f_{\text{p}}}$为临界干摩擦力。

式中${\mu _2}$为碰摩环与摩擦片之间的摩擦因数，${f_{\text{s}}}$为单个弹簧施加在摩擦片上的预紧力。

为了方便数值计算和分析，对变量进行无量纲化如下：${{\boldsymbol{Q}}_{\text{s}}} = \dfrac{{{{\boldsymbol{q}}_{\text{s}}}}}{e}$，${{\boldsymbol{Q}}_{\text{r}}} = \dfrac{{{{\boldsymbol{q}}_{\text{r}}}}}{e}$，${{\boldsymbol{M}}_{\text{s}}} = \dfrac{{{{\boldsymbol{m}}_{\text{s}}}}}{{{m_{\text{n}}}}}$，${{\boldsymbol{M}}_{\text{r}}} = \dfrac{{{{\boldsymbol{m}}_{\text{r}}}}}{{{m_{\text{n}}}}}$，${{\boldsymbol{K}}_{\text{s}}} = \dfrac{{{{\boldsymbol{k}}_{\text{s}}}}}{{{k_{\text{n}}}}}$，${{\boldsymbol{C}}_{\text{s}}} = \dfrac{{{{\boldsymbol{c}}_{\text{s}}}}}{{\sqrt {{k_{\text{n}}}{m_{\text{n}}}} }}$，${{\boldsymbol{G}}_{\text{s}}} = \dfrac{{{{\boldsymbol{g}}_{\text{s}}}}}{{{m_{\text{n}}}}}$，$\varOmega = \dfrac{{\dot \theta }}{{{\omega _{\text{n}}}}}$，$\tau = {\omega _{\text{n}}}t$，${K_1} = \dfrac{{{k_1}}}{{{k_{\text{n}}}}}$，$\varDelta { _1} = \dfrac{{{\delta _1}}}{e}$，${F_{\text{p}}}{\text{ = }}\dfrac{{{f_{\text{p}}}}}{{{k_{\text{n}}}e}}$。其中${m_{\text{n}}}$、${k_{\text{n}}}$与${\omega _{\text{n}}}$满足${\omega _{\text{n}}} = \sqrt {\dfrac{{{k_{\text{n}}}}}{{{m_{\text{n}}}}}}$，${\omega _{\text{n}}}$为传动轴1阶固有频率，${k_{\text{n}}}$近似取载荷作用于传动轴中心处的等效刚度大小。传动轴1阶固有频率及等效刚度均可通过理论计算获得^[21]。

2.   典型响应结果分析

2.1   未安装减振器时的响应结果

采用某型直升机尾传动轴参数进行数值仿真^[22]，传动轴参数如表1所示。

表  1  空心传动轴参数

Table  1.  Parameters of the hollow shaft

参数	数值
长度L/mm	2600
内径d/mm	111
外径D/mm	114.2
密度ρ/（kg/m3）	2800
弹性模量E/GPa	71
偏心量e/mm	0.3

下载: 导出CSV 

| 显示表格

经过理论计算${k_{\text{n}}}$取180 kN/m。设轴承处支承刚度为700 kN/m，阻尼系数为1500 N/（m/s）^[23]。

为了激发出传动轴的2阶模态，将偏心激励作用在节点5即1/4节点。将传动轴转速从0匀加速到5.5倍的临界转速，得到未安装限幅减振器时的传动轴瞬态响应结果。

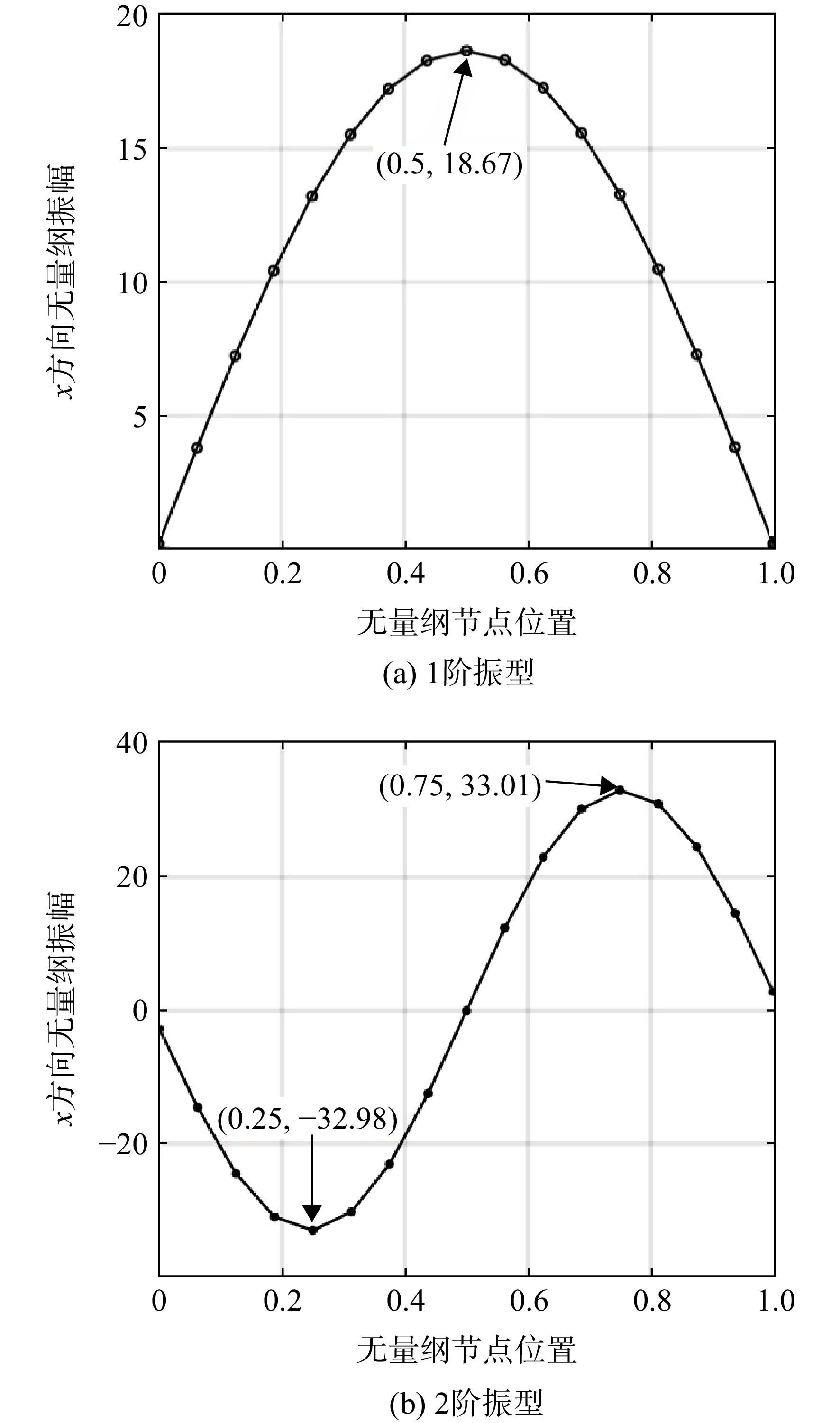
图4给出了传动轴过1阶临界转速的振型及过2阶临界转速的振型。图中横坐标为无量纲节点位置，表示节点位置与传动轴长度的比值；纵坐标为无量纲振幅。从图4（a）中可以看出，传动轴过1阶临界转速时，节点9即传动轴中间节点处振幅最大。从图4（b）中可以看出，传动轴过2阶临界转速时振动最大的位置在节点5及节点13即1/4节点处。

图  4  传动轴跨临界振型

Figure  4.  Mode shapes of the shaft as crossing through critical speeds

下载: 全尺寸图片 幻灯片

2.2   安装减振器时的典型过临界响应

以传动轴过1阶临界转速的运动过程为例，对安装限幅减振器后的传动轴典型过临界运动过程进行分析。进一步结合工程实际应用经验及以往仿真结果^[21]，设置限幅减振器的无量纲参数如表2所示。

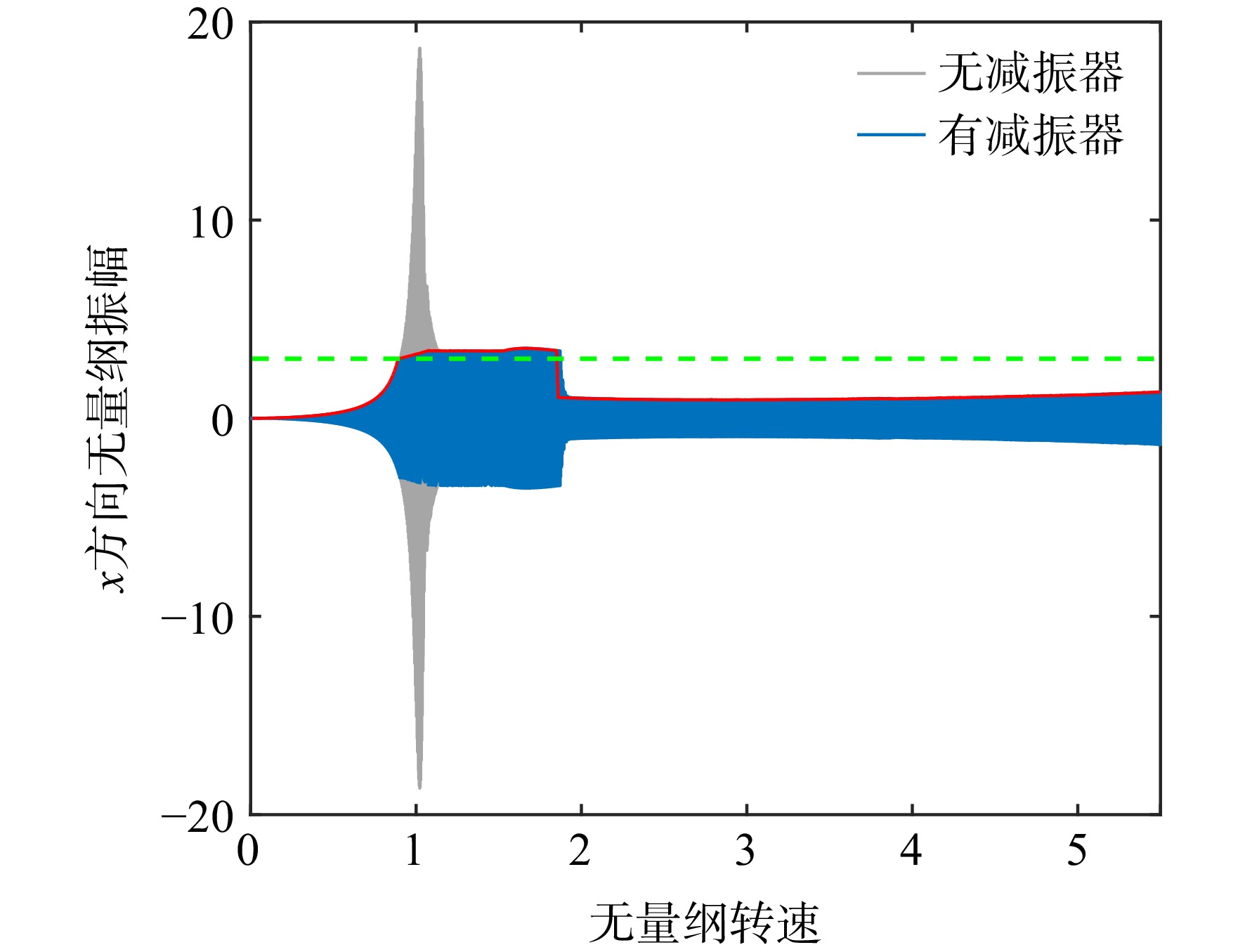
表  2  限幅减振器相关无量纲参数设定

Table  2.  Dimensionless parameters of the dry friction damper

参数	数值
无量纲碰摩环质量Mr	0.05
传动轴与碰摩环无量纲法向碰摩刚度K1	15
传动轴与碰摩环切向碰摩摩擦因数${\mu _1}$	0.1
传动轴与碰摩环无量纲初始间隙Δ1	3
无量纲临界干摩擦力Fp	6

下载: 导出CSV 

| 显示表格

将减振器安装在节点9，以观察减振器对传动轴跨1阶临界转速的减振过程。图5给出了传动轴节点9的位移响应曲线，为了进行比较，图中也给出了无减振器时的位移曲线。图中绿色虚线表示$\varDelta { _1}$的大小，红色曲线为传动轴的幅频特性曲线。从图中可以看出，在限幅减振器的作用下，传动轴过临界转速的振动大大减小。

图  5  节点9响应

Figure  5.  Response of node 9

下载: 全尺寸图片 幻灯片

为了进一步研究传动轴过临界过程中的动力学特性，通过分岔图及频率瀑布图对传动轴运动过程进行频率分析。无量纲转速从0.01增加到5.5，以上一个激励频率下的系统末状态作为下一个激励下的系统初状态，得到传动轴频率响应结果。以转速作为变量，绘制分岔图。图6给出了传动轴过1阶临界转速过程中节点9分岔图及幅频特性曲线，图7给出了节点9频率瀑布图。

图  6  节点9分岔图及幅频特性曲线

Figure  6.  Bifurcation diagram and amplitude frequency characteristic curve of node 9

下载: 全尺寸图片 幻灯片

图  7  节点9频率瀑布图

Figure  7.  Waterfall frequency response spectrum of node 9

下载: 全尺寸图片 幻灯片

根据图6中的仿真结果，将传动轴跨临界转速的运动过程分为4个阶段，分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ。

在阶段Ⅰ，传动轴振动较小，未与减振器发生碰摩。图8（a）给出了无量纲频率为0.8时的轴心轨迹图及庞加莱截面，蓝色曲线为轴心轨迹，黑色圆点为庞加莱截面。传动轴的轴心轨迹始终在间隙${\varDelta _{{\text{ 1}}}}$（红色虚线）以内，庞加莱截面图为一个点，说明传动轴处于单周期运动状态。

图  8  轴心轨迹及庞加莱截面图

Figure  8.  Whirling orbits and Poincare maps

下载: 全尺寸图片 幻灯片

在阶段Ⅱ，传动轴超越初始间隙并与碰摩环发生碰摩，但由于碰摩力较小，碰摩环并未完全运动起来。图8（b）给出了无量纲频率为1.1时节点9的轴心轨迹图及庞加莱截面图，可以看出传动轴处于拟周期运动状态。同时从图7中也可以看出传动轴响应在这1阶段出现高频成分。

在阶段Ⅲ，碰摩环在较大的碰摩力作用下克服临界干摩擦力发生滑动。图8（c）给出了无量纲频率为1.7时节点9的轴心轨迹图及庞加莱截面图。可以看出此时传动轴发生同频全周碰摩，处于单周期运动状态。

从阶段Ⅲ到阶段Ⅳ，传动轴发生跳跃现象，此时的转速为传动轴的跳跃转速。在阶段Ⅳ，传动轴与碰摩环脱离碰摩，处于单周期运动状态，如图8（d）所示。需要指出的是，当传动轴正常工作转速给定后，跳跃转速应低于正常工作转速，避免碰摩持续发生，影响传动轴的正常运转，且跳跃转速越小，传动轴正常运转的安全裕度越大。

从以上对传动轴节点9跨1阶临界转速运动过程的分析可以看出，在碰摩环黏滞阶段，传动轴与碰摩环之间发生拟周期碰摩，系统的稳定性较差。由于碰摩环的滑动，系统由拟周期碰摩运动发展为同频全周碰摩运动，稳定性增强。限幅减振器发挥作用主要在阶段Ⅱ和阶段Ⅲ。在阶段Ⅱ，碰摩环黏滞，对传动轴振动产生限位作用；在阶段Ⅲ，碰摩环发生滑动，引入了干摩擦阻尼消耗振动能量，实现对传动轴的减振。

传动轴跨2阶临界转速的运动过程与上述运动过程保持一致，但由于2阶振动较大，因此在拟周期阶段会发生更为剧烈的碰摩，这里就不再进行赘述。

3.   安装位置对减振效果的影响

根据以上对传动轴典型过临界响应的分析，限幅减振器的减振效果从两方面进行评估，一方面传动轴的跨临界振幅得到有效抑制，另一方面传动轴的跳跃转速尽可能小。考虑到传动轴跨1阶临界转速时节点9振幅最大，跨2阶临界转速时节点5振幅最大，因此分别将限幅减振器安装在节点9、节点5及两者之间的节点7即3/8节点，如图9所示。此外，从文中第2.2节的分析中知道，限幅减振器主要通过碰摩环黏滞阶段的限幅作用及碰摩环滑动阶段的干摩擦阻尼实现减振，而这两方面的减振作用均与临界干摩擦力值息息相关。因此考虑在某一特定的安装位置下分别调节不同的临界干摩擦力，观察限幅减振器所能达到的减振效果。本节通过给出传动轴跨1阶及2阶临界转速的振型及节点5、节点9的瞬态响应，对传动轴的响应结果进行分析。

图  9  减振器安装位置示意图

Figure  9.  Illustration location diagram of the damper

下载: 全尺寸图片 幻灯片

3.1   减振器安装在节点9

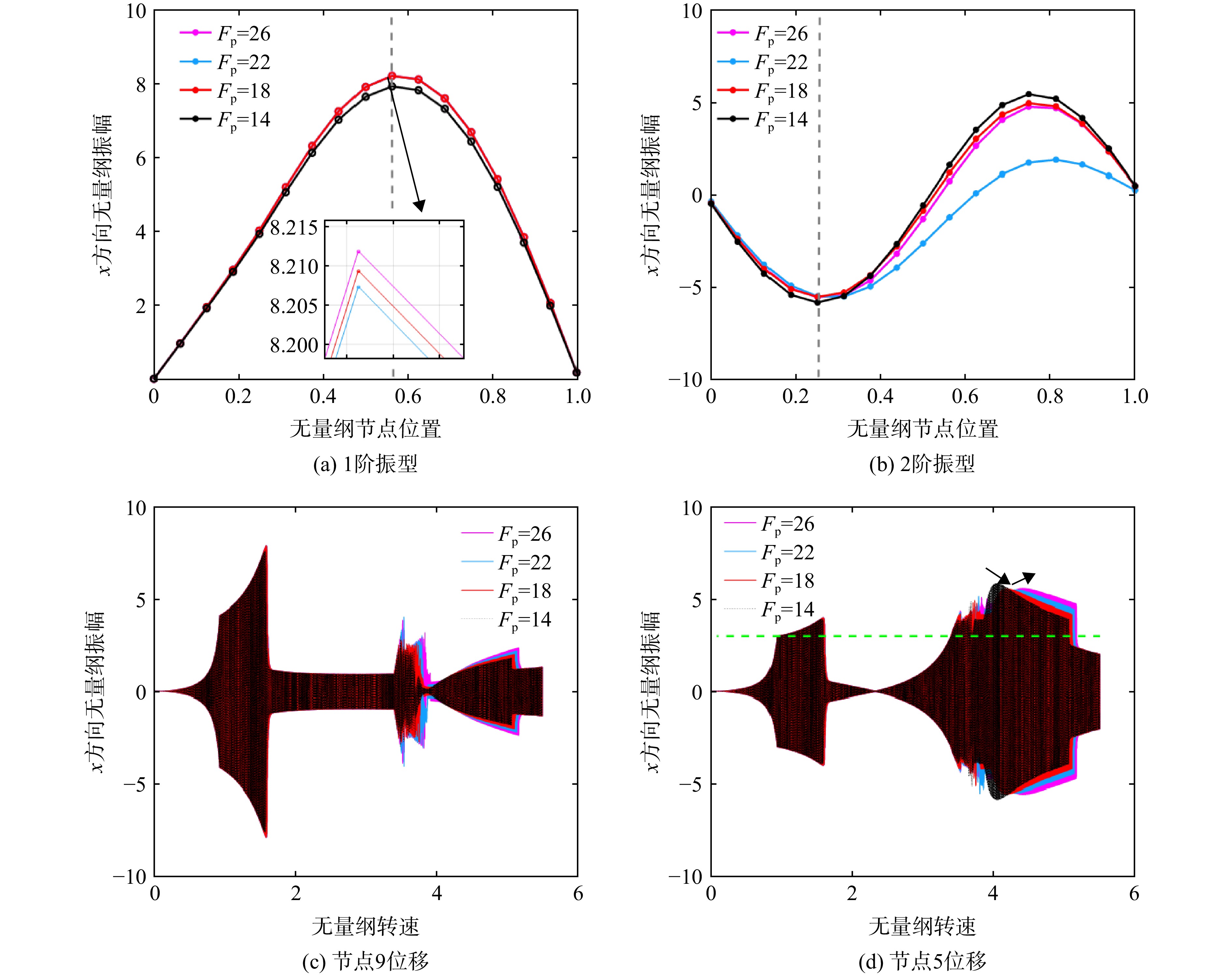
图10给出了减振器安装在节点9时，在不同临界干摩擦力下的传动轴响应结果。从图中可以看出，与图4中未安装减振器的结果相比，传动轴跨1阶临界转速的振幅得到了有效抑制，且随着临界干摩擦力的增加先减小后增大，存在一个最优临界干摩擦力使1阶振幅最小；随着临界干摩擦力的增加，1阶跳跃转速增大。在不同的临界干摩擦力下，传动轴跨2阶临界转速的响应曲线基本重合且振幅很大，减振器对传动轴过2阶临界转速没有减振作用，这是由传动轴本身的2阶振型决定的。

图  10  减振器安装在节点9时的传动轴响应

Figure  10.  Responses of the shaft when the damper is located at node 9

下载: 全尺寸图片 幻灯片

3.2   减振器安装在节点5

将减振器安装在节点5，考虑到传动轴的2阶振动较1阶振动更为剧烈，因此增大临界干摩擦力，传动轴的响应结果如图11所示。图11（b）、图11（d）与图10（b）、图10（d）中的响应结果相比较可以看出，传动轴跨2阶临界转速的振动得到了有效抑制。节点5的2阶振幅随临界干摩擦力的增加先减小后增大，存在最优临界干摩擦力使2阶幅值最小。另外，从图11（d）可以看出，随着临界干摩擦力的增大，跳跃转速增大。但图11（a）、图11（c）与图10（a）、图10（c）中的结果相比，显然较大的临界干摩擦力使传动轴1阶振幅增大。

图  11  减振器安装在节点5时的传动轴响应

Figure  11.  Responses of the shaft when the damper is located at node 5

下载: 全尺寸图片 幻灯片

3.3   减振器安装在节点7

进一步考虑将减振器安装在节点7，同样调节临界干摩擦力，传动轴的响应结果如图12所示。为了观察传动轴与减振器之间的碰摩情况，同时给出了节点7的瞬态响应结果。

图  12  减振器安装在节点7时的传动轴响应

Figure  12.  Responses of the shaft when the damper is located at node 7

下载: 全尺寸图片 幻灯片

从图中可以看出，传动轴跨1阶及2阶临界转速的振动均得到了有效抑制，且存在最优临界干摩擦力使节点5的2阶振幅最小。但与安装在节点5相比，其对过2阶临界的减振作用减弱，且使振幅最小的最优临界干摩擦力值发生变化。此外，仿真发现当临界干摩擦力较小（图12中${F_{\text{p}}} = 14$）时，传动轴跨2阶临界转速后与碰摩环持续发生碰摩；当临界干摩擦力较大时，传动轴“跳跃”之后又会与减振器脱离碰摩，如图12（e）中红色虚线框内所示。一般来说，临界干摩擦力越大，越容易导致传动轴跳跃滞后，从而越不易与碰摩环脱离碰摩。而安装在节点7时，由于临界干摩擦小而导致传动轴与碰摩环无法脱离碰摩，这种现象在减振器安装在其他节点的仿真中均未发现。

因此当减振器安装在节点7时，传动轴跨1阶临界转速及2阶临界转速的振动均能得到有效抑制。但需将临界干摩擦力调大，以避免传动轴与碰摩环持续碰摩导致传动轴的正常工作受到影响。同时较大的临界干摩擦力也导致了较大的跳跃转速。

4.   结　论

本文通过建立带限幅减振器的单跨轴系有限元动力学模型，得到了传动轴典型跨临界过程的动力学响应，并对减振器安装位置对减振效果的影响进行了分析，得出了如下结论：

1） 传动轴与限幅减振器系统的跨临界运动过程可以分为4个阶段，分别为单周期无碰摩运动阶段、拟周期碰摩阶段、同频全周碰摩阶段、发生跳跃现象后回到单周期无碰摩阶段，且碰摩环的滑动有利于系统的稳定。

2） 将限幅减振器安装在中间节点，可以对传动轴过1阶临界转速产生很好的减振作用，但对传动轴过2阶临界转速没有减振效果。安装在1/4节点及3/8节点处，将临界干摩擦力增大，对传动轴跨1阶及2阶临界转速的振动均能起到抑制作用；但与安装在中间节点相比，对跨1阶临界转速的减振作用减弱；同时较大的临界干摩擦力也导致了较大的跳跃转速。另外，将减振器安装在3/8节点处，当临界干摩擦力较小时，传动轴无法与碰摩环脱离碰摩导致其正常工作受到影响。