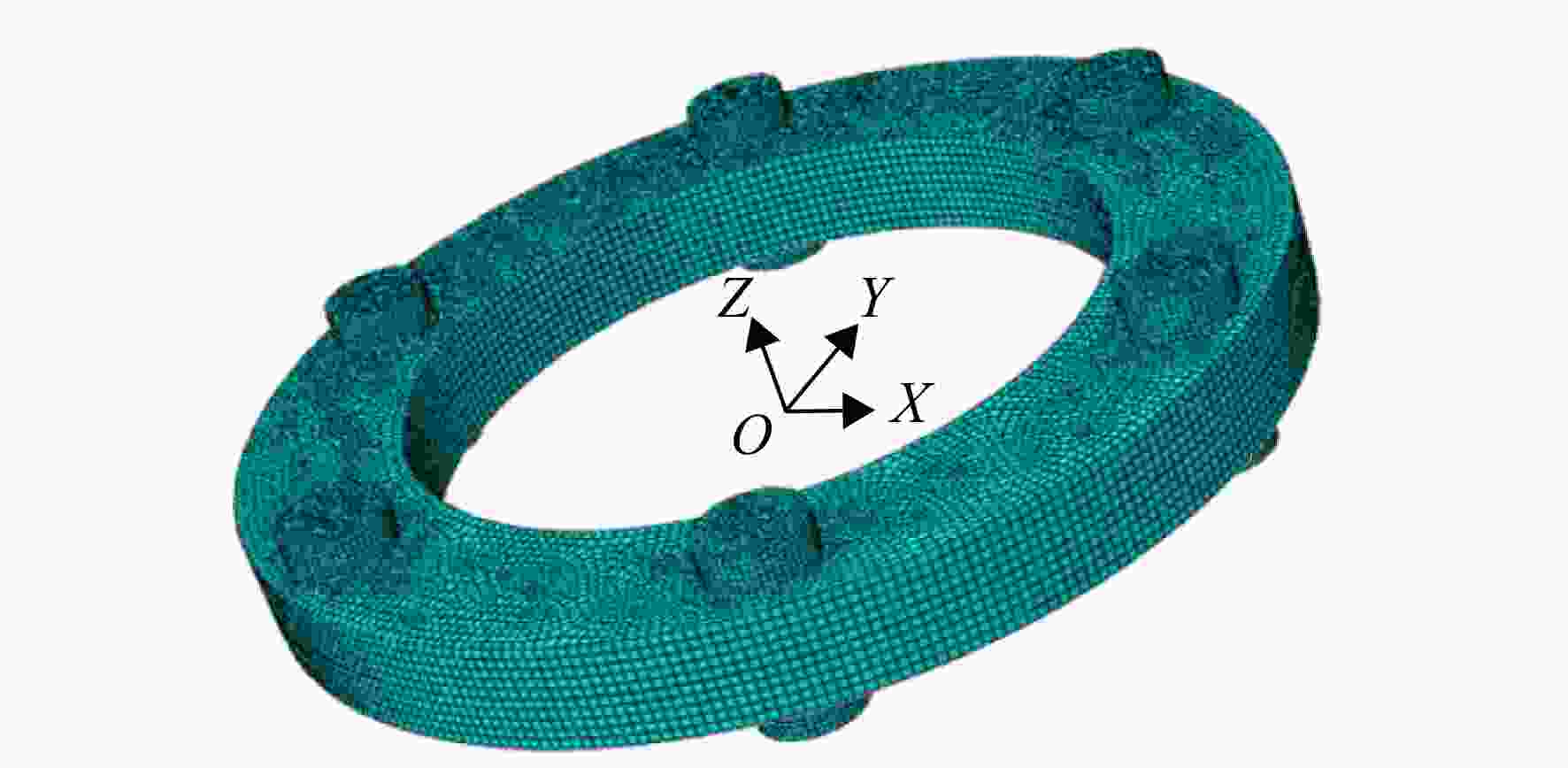
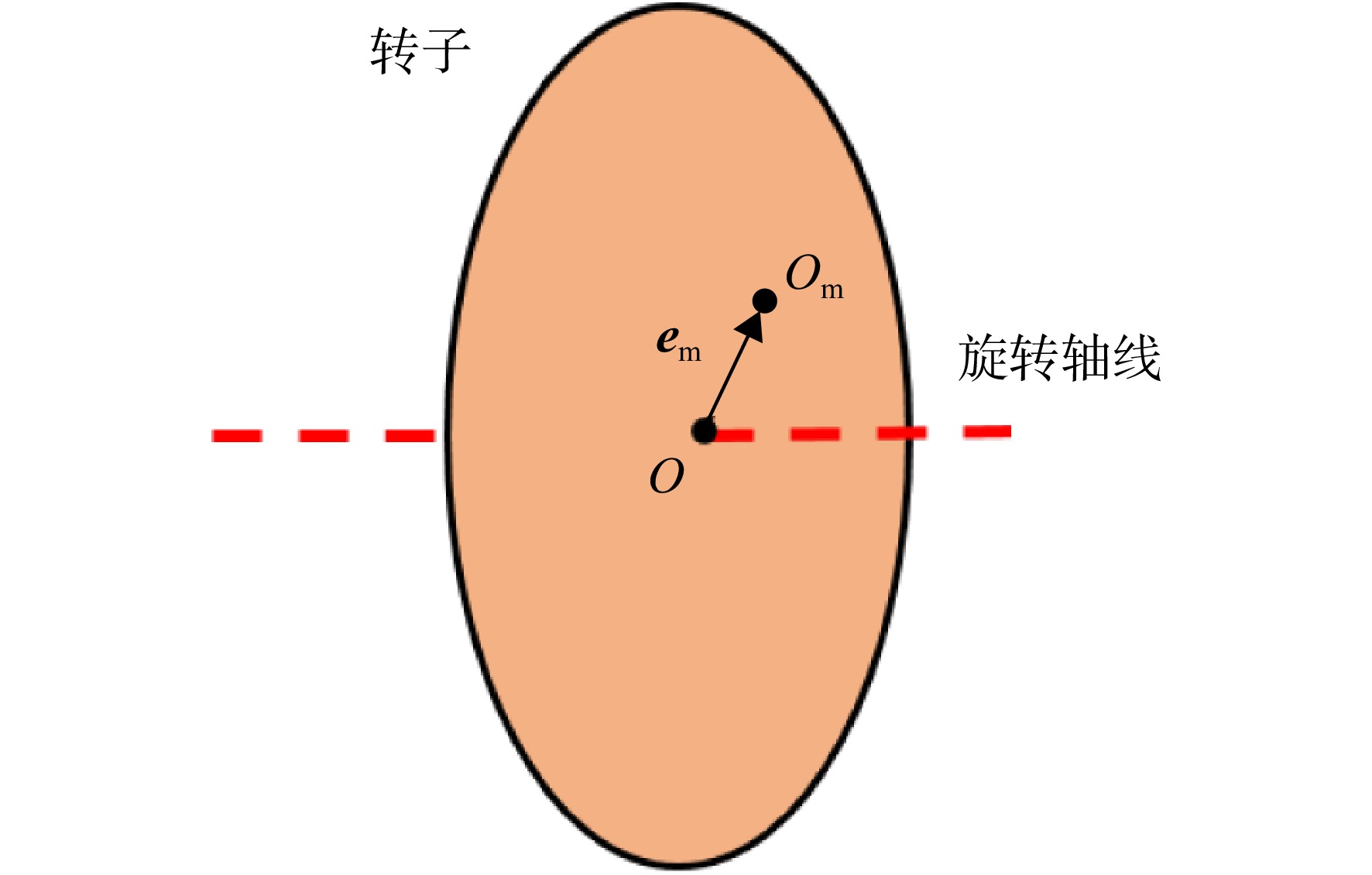
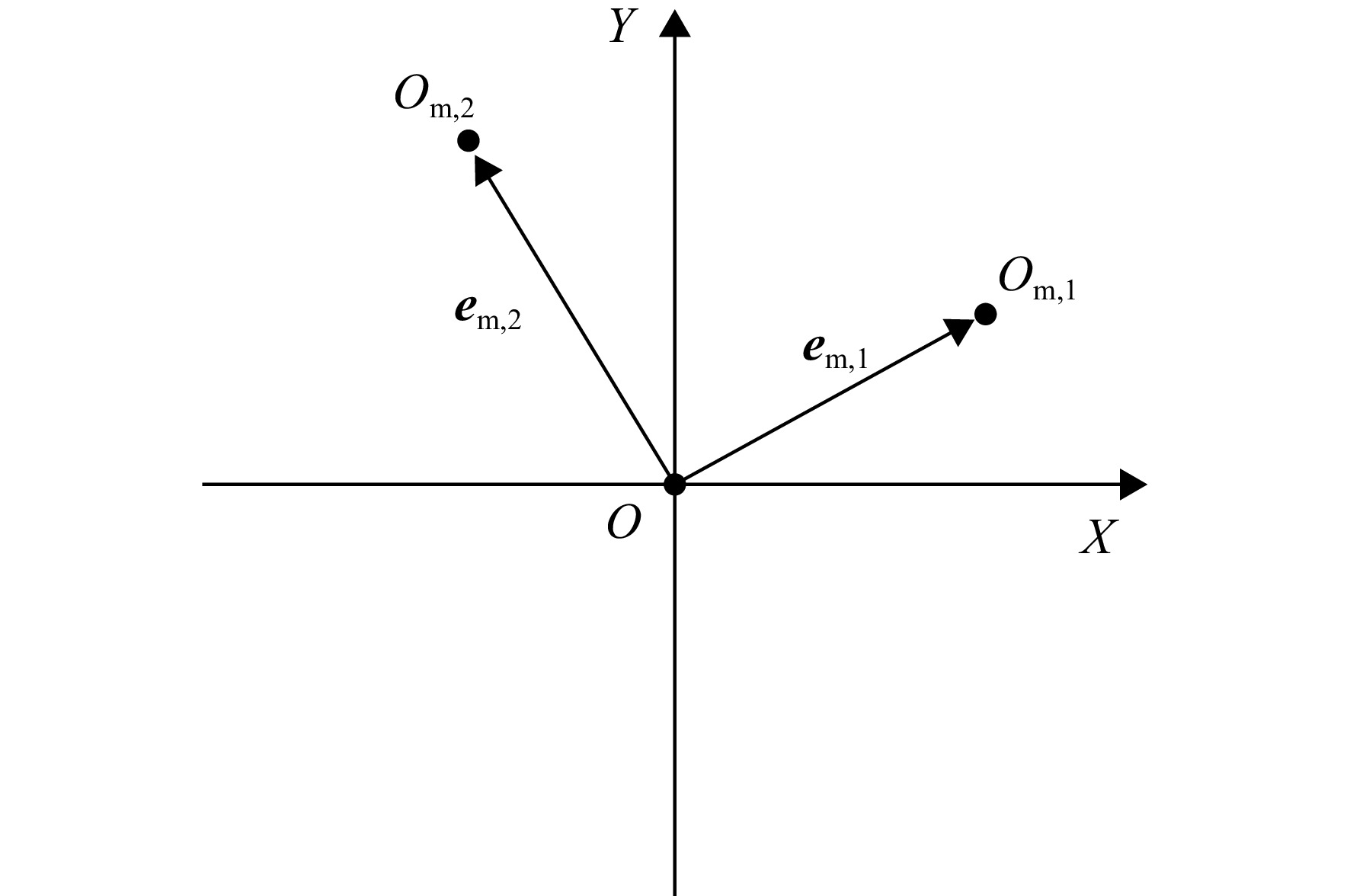
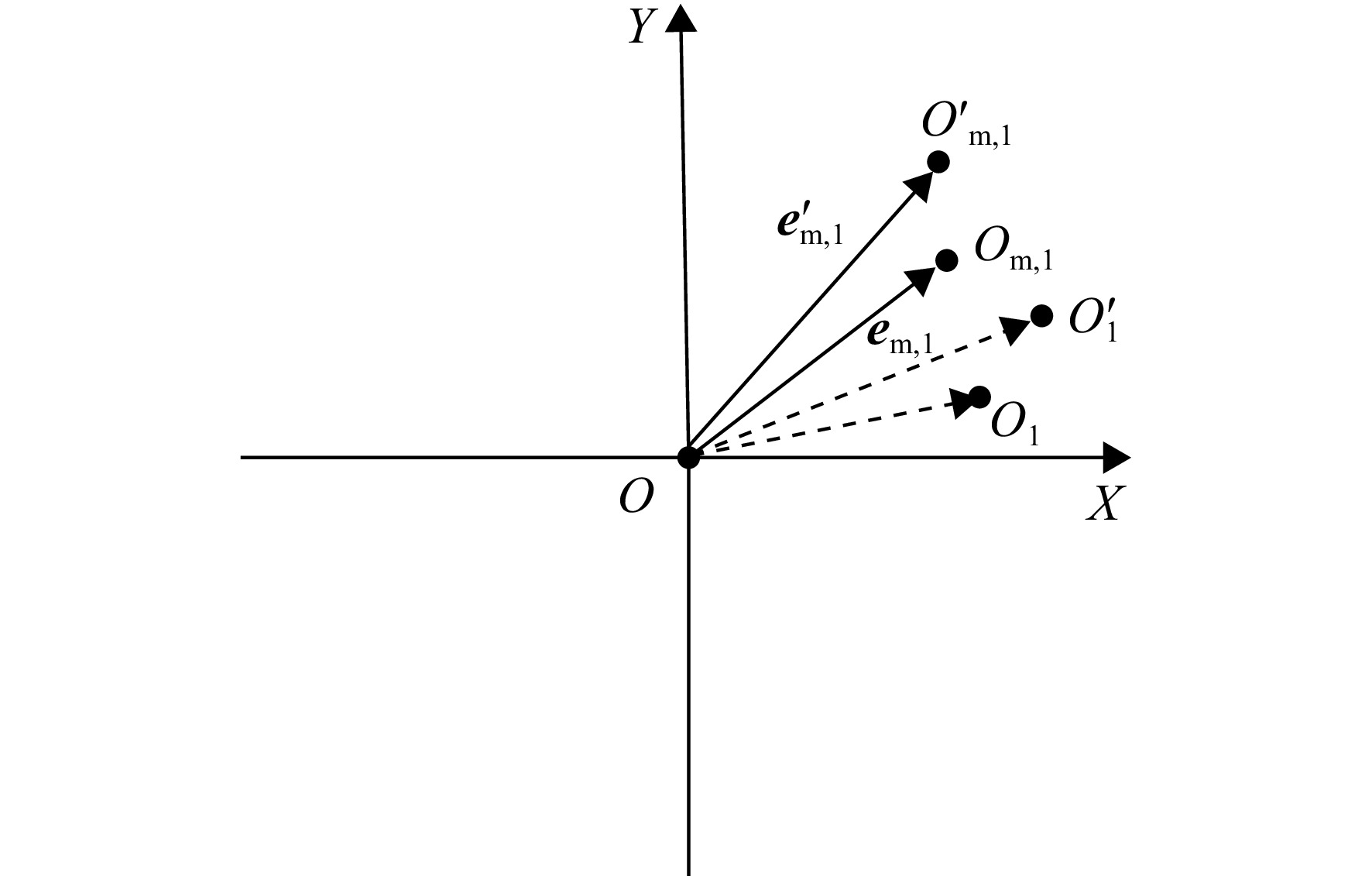
Prediction of assembly eccentricity and optimization of installation phase for short precision bolted connection structures
-
摘要:
为了有效提高短精密螺栓连接结构的装配精度，分析了两级盘组合后形心、质心偏心影响因素，阐述了两级盘配合过程中的平动转动行为和定心原理，建立了两级转子形心偏差预测模型、初始不平衡量预测模型。提出了以短精密螺栓连接的转子盘安装相位为变量，形心偏心和初始不平衡量最小为优化为目标的工艺优化模型，通过实物实验进行了验证。结果表明：形心偏差模长最大相对误差为13.28%，组合不平衡量的计算结果精度最大提高了37.3%，工艺优化结果与实验结果相符，对于短精密螺栓连接结构装配工艺优化具有重要的参考意义。
Abstract:In order to effectively improve the assembly accuracy of the short precision bolted connection structures, the influencing factors of the centroid and centroid eccentricity after combination of the two-stage disks were analyzed, the translational rotation behavior and centering principle during the matching process of the two-stage disks were expounded, and a two-stage rotor was established. Centroid deviation prediction model and initial imbalance prediction model were established. A process optimization model was proposed, the installation phase of the rotor disk connected by short precision bolts was taken as the variable, and the centroid eccentricity and the mini-mum initial unbalance amount were taken as the optimization objective, which were verified by the physical test. The results showed that the maximum relative error of the module length of the centroid deviation was 13.28%, the maximum accuracy of the calculation result of the combined unbalance increased by 37.3%, and the process optimization results were consistent with the test results, which had important reference significance for the optimization of the assembly process of short precision bolted connection structures.
-
Key words:
- short precision bolt /
- concentricity /
- unbalance /
- installation phase /
- process optimization
-
图 5 质心与旋转轴线不重合示意图
Figure 5. Schematic diagram of misalignment of center of mass and axis of rotation
表 1 精密螺栓孔的偏心偏差
Table 1. Eccentricity deviation of precision bolt holes
螺栓孔编号 偏心距/mm 偏心角/（°） 1 0.020 202 2 0.024 166 3 0.016 68 4 0.018 131 5 0.020 102 6 0.022 105 
下载: 导出CSV
表 2 偏心计算结果
Table 2. Eccentricity calculation results
X分量/mm Y分量/mm 偏心距/mm 偏心角/（°） 0.00811 −0.00978 0.01271 −50.3512
下载: 导出CSV
表 3 零件B的形心坐标
Table 3. Part B centroid coordinates
mm 工况 X分量 Y分量 仿真前 −1.701×10−5 −0.516×10−5 仿真后 0.00774 −0.00956
下载: 导出CSV
表 4 偏心距、偏心角结果对比
Table 4. Comparison of eccentric distance and eccentric angle results
参数 绝对误差 相对误差/% 偏心距/mm 0.000 41 3.33 偏心角/（°） 0.6528
下载: 导出CSV
表 5 转子零件测量数据拟合结果
Table 5. Fitting results of measured data of rotor parts
mm 位置 拟合中心 半径 X分量 Y分量 一级转
实验件1号孔 139.9886 0 3.1797 7号孔 −70.01658 −121.22245 3.1798 13号孔 −70.00579 121.25805 3.1794 二级转
实验件1号孔 139.98860 0 3.1797 7号孔 −70.01755 −121.24723 3.1801 13号孔 −70.00201 121.23842 3.1802 轴颈柱面 0.00055 −0.03252 129.49418
下载: 导出CSV
表 6 轴颈中心计算结果
Table 6. Calculation result of journal center
方案 预测中心坐标/mm 模长/mm 相位/（°） X分量 Y分量 1-1 −0.00158 −0.01772 0.01779 264.90 1-7 0.00775 0.03607 0.03689 77.87 1-13 −0.04349 0.01725 0.04679 158.36
下载: 导出CSV
表 7 转子零件初始不平衡量
Table 7. Initial unbalance of rotor parts
位置 不平衡
质量/mg半径/
mm相位/
（°）静不平衡量/
（g·mm）一级转子实验件 490 104 157 50.96 二级转子实验件 1 902 104 76 197.808
下载: 导出CSV
表 8 不同安装相位下第二级转子不平衡量
Table 8. Second-stage rotor unbalance under different installation phases
方案 质心位置/mm 静不平衡量/（g·mm） 相位/（°） 1-1 0.13567 197.808 76 1-7 0.13908 202.779 183.64 1-13 0.11100 161.838 308.21
下载: 导出CSV
表 9 不同安装相位组合不平衡量预测结果
Table 9. Combined unbalance prediction results under different installation phases
方案 组合不平衡量/（g·mm） 相位/（°） 1-1 211.85 89.8 1-7 249.38 178.38 1-13 119.72 296.38
下载: 导出CSV
表 10 可行解列表
Table 10. List of feasible solution
可行解方案 偏心误差/mm 组合不平衡量/（g·mm） 1-1 0.01779 211.85
下载: 导出CSV
表 11 轴颈中心测量结果
Table 11. Measurement results of journal center
方案 拟合中心坐标/mm 模长/mm 相位/（°） X分量 Y分量 1-1 −0.00351 −0.01922 0.01954 259.65 1-7 0.01254 0.04066 0.04254 73.62 1-13 −0.04190 0.02848 0.05066 145.80
下载: 导出CSV
表 12 计算结果与实验结果比较
Table 12. Comparing of calculated results with experimental results
方案 模长相对误差/% 相位绝对误差/（°） 1-1 8.96 5.25 1-7 13.28 4.25 1-13 7.64 12.56
下载: 导出CSV
表 13 不平衡量测量数据
Table 13. Unbalance measurement data
方案 不平衡
质量/mg半径/mm 组合不平
衡量/（g·mm）相位/（°） 1-1 2036 104 211.744 90 1-7 2389 248.456 172 1-13 858 89.232 286
下载: 导出CSV
表 14 计算结果误差
Table 14. Calculation result error
方案 不考虑装配偏差 考虑装配偏差 不平衡量
相对误差/%相位绝对
误差/（°）不平衡量
相对误差/%相位绝对
误差/（°）1-7 3.6 16.30 0.4 6.38 1-13 69.5 23.40 34.2 10.38
下载: 导出CSV
表 15 优化结果对比
Table 15. Optimization results comparison
项目 方案1-1预测值 方案1-1实测值 误差 偏心量 模长 0.01779 mm 0.01954 mm 8.96% 相位/（°） 264.9 259.65 5.25 组合不平
衡量数值 211.85 g·mm 211.744 g·mm 0.4% 相位/（°） 89.8 90 0.2
下载: 导出CSV
-
[1] 陈光,洪杰,马艳红. 航空燃气涡轮发动机结构[M]. 北京: 北京航空航天大学出版社,2010. [2] 张渝,李琳,陈津,等. 航空发动机重要装配工艺分析及研发展望[J]. 航空制造技术,2019,62(15): 14-21. ZHANG Yu,LI Lin,CHEN Jin,et al. Research Current status and prospect on aero-engine assembly process technology[J]. Aeronautical Manufacturing Technology,2019,62(15): 14-21. (in Chinese doi: 10.16080/j.issn1671-833x.2019.15.014 ZHANG Yu, LI Lin, CHEN Jin, et al . Research Current status and prospect on aero-engine assembly process technology[J]. Aeronautical Manufacturing Technology,2019 ,62 (15 ):14 -21 . (in Chinese) doi: 10.16080/j.issn1671-833x.2019.15.014[3] 章伊华,庞奎,林丹益,等. 基于接触面特征的螺栓联接刚度研究[J]. 兵工学报,2017,38(1): 195-201. ZHANG Yihua,PANG Kui,LIN Danyi,et al. Study of bolt joint stiffness based on contact surface characteristics[J]. Acta Armamentarii,2017,38(1): 195-201. (in Chinese ZHANG Yihua, PANG Kui, LIN Danyi, et al . Study of bolt joint stiffness based on contact surface characteristics[J]. Acta Armamentarii,2017 ,38 (1 ):195 -201 . (in Chinese)[4] 焦俊杰,莫蓉,徐广庆,等. 螺栓孔的位置度误差对短精密螺栓连接结构装配力学特性的影响[J]. 航空动力学报,2021,36(5): 935-947. JIAO Junjie,MO Rong,XU Guangqing,et al. Influence of position error of bolt hole on assembly mechanical characteristics of short precision bolted connection structure[J]. Journal of Aerospace Power,2021,36(5): 935-947. (in Chinese JIAO Junjie, MO Rong, XU Guangqing, et al . Influence of position error of bolt hole on assembly mechanical characteristics of short precision bolted connection structure[J]. Journal of Aerospace Power,2021 ,36 (5 ):935 -947 . (in Chinese)[5] 李泽林. 基于轴向预载的转子装配方法研究[D]. 哈尔滨: 哈尔滨工业大学,2018. LI Zelin. Research on rotor assembly method based on axial compression[D]. Harbin: Harbin Institute of Technology,2018. (in ChineseLI Zelin. Research on rotor assembly method based on axial compression[D]. Harbin: Harbin Institute of Technology, 2018. (in Chinese) [6] LI X D,CHEN J,SUN K P,et al. Research on pre-tensioning process of low-pressure turbine shaft assembly for aeroengines considering the rabbet joint structure[J]. International Journal of Smart Engineering,2019,3(1): 23-34. [7] DING Siyi,JIN Sun,LI Zhimin,et al. Multistage rotational optimization using unified Jacobian–Torsor model in aero-engine assembly[J]. Proceedings of the Institution of Mechanical Engineers,Part B: Journal of Engineering Manufacture,2019,233(1): 251-266. [8] 丁司懿,金隼,李志敏,等. 航空发动机转子装配同心度的偏差传递模型与优化[J]. 上海交通大学学报,2018,52(1): 54-62. DING Siyi,JIN Sun,LI Zhimin,et al. Deviation propagation model and optimization of concentricity for aero-engine rotor assembly[J]. Journal of Shanghai Jiao Tong University,2018,52(1): 54-62. (in Chinese DING Siyi, JIN Sun, LI Zhimin, et al . Deviation propagation model and optimization of concentricity for aero-engine rotor assembly[J]. Journal of Shanghai Jiao Tong University,2018 ,52 (1 ):54 -62 . (in Chinese)[9] 高一超. 航空发动机转子装配精度预测及相位优化方法研究[D]. 大连: 大连理工大学,2020: 42-48. GAO Yichao. Research on accuracy prediction and phase optimization of aeroengine rotor assembly[D]. Dalian: Dalian University of Technology,2020: 42-48. (in ChineseGAO Yichao. Research on accuracy prediction and phase optimization of aeroengine rotor assembly[D]. Dalian: Dalian University of Technology, 2020: 42-48. (in Chinese) [10] 张伟,陈爽,杜双言,等. 制造误差对航发转子同心度的影响[J]. 现代制造技术与装备,2021,57(8): 26-29. ZHANG Wei,CHEN Shuang,DU Shuangyan,et al. Effecet of manufacturing error on the concentricity of aero engine rotor[J]. Modern Manufacturing Technology and Equipment,2021,57(8): 26-29. (in Chinese ZHANG Wei, CHEN Shuang, DU Shuangyan, et al . Effecet of manufacturing error on the concentricity of aero engine rotor[J]. Modern Manufacturing Technology and Equipment,2021 ,57 (8 ):26 -29 . (in Chinese)[11] ZHANG W,YE Y S,CHEN D A,et al. Numerical analysis of bolt elastic interaction in non-gasketed flange[R]. Prague,Czech: ASME 2018 Pressure Vessels and Piping Conference,2018. [12] 叶永松. 考虑实际接触的螺栓止口连接预紧力及其变形研究[D]. 大连: 大连理工大学,2019: 44-48. YE Yongsong. Study on pre-tightening force and deformation of bolted connection with rabbet considering actual contact[D]. Dalian: Dalian University of Technology,2019: 44-48. (in ChineseYE Yongsong. Study on pre-tightening force and deformation of bolted connection with rabbet considering actual contact[D]. Dalian: Dalian University of Technology, 2019: 44-48. (in Chinese) [13] 张子豪,郭俊康,洪军,等. 航空发动机高压转子装配偏心预测和相位优化的智能算法应用研究[J]. 西安交通大学学报,2021,55(2): 47-54. ZHANG Zihao,GUO Junkang,HONG Jun,et al. Application study of intelligent algorithms for prediction and phase optimization of assembly eccentricity of aero-engine high pressure rotor[J]. Journal of Xi’an Jiaotong University,2021,55(2): 47-54. (in Chinese ZHANG Zihao, GUO Junkang, HONG Jun, et al . Application study of intelligent algorithms for prediction and phase optimization of assembly eccentricity of aero-engine high pressure rotor[J]. Journal of Xi’an Jiaotong University,2021 ,55 (2 ):47 -54 . (in Chinese)[14] 陈爽. 螺栓-止口连接的安装边制造误差对装配性能的影响研究[D]. 大连: 大连理工大学,2021: 31-38. CHEN Shuang. Research on the influence of manufacturing error of mounting edge of bolt-stop connection on the assembly performance[D]. Dalian: Dalian University of Technology,2021: 31-38. (in ChineseCHEN Shuang. Research on the influence of manufacturing error of mounting edge of bolt-stop connection on the assembly performance[D]. Dalian: Dalian University of Technology, 2021: 31-38. (in Chinese) [15] 侯博文. 真实接触表面形貌下螺栓连接结构的力学性能[D]. 大连: 大连理工大学,2020: 25-38. HOU Bowen. Mechanical properties of bolted connection structure under real contact surface topography[D]. Dalian: Dalian University of Technology,2020: 25-38. (in ChineseHOU Bowen. Mechanical properties of bolted connection structure under real contact surface topography[D]. Dalian: Dalian University of Technology, 2020: 25-38. (in Chinese) [16] HOU B W,SUN Y D,SUN W,et al. The properties of bolted joint assembly with contact stiffness[J]. International Journal of Smart Engineering,2018,2(3): 325-342. [17] WANG Xiaoming,CAO Zifei,SUN Chuanzhi,et al. Positioning and orientation error measurement and assembly coaxiality optimization in rotors with curvic couplings[J]. Measurement,2021,186: 110167. doi: 10.1016/j.measurement.2021.110167 [18] 刘鑫. 航空发动机转子装配精度预测及堆叠[D]. 大连: 大连理工大学,2019: 30-34. LIU Xin. Assembly accuracy prediction and stacking of aeroengine rotor[D]. Dalian: Dalian University of Technology,2019: 30-34. (in ChineseLIU Xin. Assembly accuracy prediction and stacking of aeroengine rotor[D]. Dalian: Dalian University of Technology, 2019: 30-34. (in Chinese) [19] 琚奕鹏,吴法勇,金彬,等. 基于转子跳动和初始不平衡量优化的多级盘转子结构装配工艺[J]. 航空发动机,2018,44(6): 83-90. JU Yipeng,WU Fayong,JIN Bin,et al. Structure assembly technique of multi-stage disc rotor based on rotor runout and unbalance optimization[J]. Aeroengine,2018,44(6): 83-90. (in Chinese JU Yipeng, WU Fayong, JIN Bin, et al . Structure assembly technique of multi-stage disc rotor based on rotor runout and unbalance optimization[J]. Aeroengine,2018 ,44 (6 ):83 -90 . (in Chinese)[20] 刘君,吴法勇,王娟. 航空发动机转子装配优化技术[J]. 航空发动机,2014,40(3): 75-78. LIU Jun,WU Fayong,WANG Juan. Optimization technique of aeroengine rotor assembly[J]. Aeroengine,2014,40(3): 75-78. (in Chinese doi: 10.13477/j.cnki.aeroengine.2014.03.016 LIU Jun, WU Fayong, WANG Juan . Optimization technique of aeroengine rotor assembly[J]. Aeroengine,2014 ,40 (3 ):75 -78 . (in Chinese) doi: 10.13477/j.cnki.aeroengine.2014.03.016[21] 刘洪慧,刘亮,李明华,等. 多级盘转子装配不平衡量预测与优化[J]. 机械科学与技术,2022,41(8): 1298-1305. LIU Honghui,LIU Liang,LI Minghua,et al. Prediction and optimization of assembly unbalance of multi-stage disc rotor[J]. Mechanical Science and Technology for Aerospace Engineering,2022,41(8): 1298-1305. (in Chinese LIU Honghui, LIU Liang, LI Minghua, et al . Prediction and optimization of assembly unbalance of multi-stage disc rotor[J]. Mechanical Science and Technology for Aerospace Engineering,2022 ,41 (8 ):1298 -1305 . (in Chinese)[22] LIU Yongmeng,ZHANG Maowei,SUN Chuanzhi,et al. A method to minimize stage-by-stage initial unbalance in the aero engine assembly of multistage rotors[J]. Aerospace Science and Technology,2019,85: 270-276. doi: 10.1016/j.ast.2018.12.007 [23] CHEN Yue,CUI Jiwen,SUN Xun. An unbalance optimization method for a multi-stage rotor based on an assembly error propagation model[J]. Applied Sciences,2021,11(2): 887. doi: 10.3390/app11020887 [24] CHEN Yue,CUI Jiwen,SUN Xun. A vibration suppression method for the multistage rotor of an aero-engine based on assembly optimization[J]. Machines,2021,9(9): 189. doi: 10.3390/machines9090189 [25] 涂建波,李震,葛浩田,等. 基于几何代数理论的转子堆叠装配多目标优化[J]. 航空学报,2021,42(10): 524197. TU Jianbo,LI Zhen,GE Haotian,et al. Multi-objective optimization of rotor-stack assembly based on geometric algebra theory[J]. Acta Aeronautica et Astronautica Sinica,2021,42(10): 524197. (in Chinese TU Jianbo, LI Zhen, GE Haotian, et al . Multi-objective optimization of rotor-stack assembly based on geometric algebra theory[J]. Acta Aeronautica et Astronautica Sinica,2021 ,42 (10 ):524197 . (in Chinese) -
点击查看大图
计量
- 文章访问数: 20
- HTML浏览量: 16
- PDF量: 3
- 被引次数: 0