推力矢量型V/STOL飞行器动态过渡过程的操纵策略优化

周涛; 王子安; 龚正; 佘崇民; 赵彤; 张同任

doi:10.13224/j.cnki.jasp.20210412

推力矢量型V/STOL飞行器动态过渡过程的操纵策略优化

doi: 10.13224/j.cnki.jasp.20210412

周涛^1,,
王子安^1,,
龚正^1,,
佘崇民¹,
赵彤²,
张同任³

1.
南京航空航天大学航空学院，南京 210016
2.
中国航空工业集团有限公司沈阳飞机设计研究所，沈阳 110000
3.
滨州学院飞行学院，山东滨州 256600

基金项目: 国家自然科学基金（11402115）；江苏高校优势学科建设工程资助项目

详细信息

作者简介:
周涛（1998-），男，硕士生，主要从事飞机飞行动力学与控制研究

中图分类号: V249.1
计量
- 文章访问数: 587
- HTML浏览量: 57
- PDF量: 304
- 被引次数: 0
出版历程
- 收稿日期: 2021-08-02
- 网络出版日期: 2022-10-24

Control strategy optimization of dynamic transition processes of thrust-vectored V/STOL aircraft

1.
College of Aerospace Engineering， Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China
2.
Shenyang Aircraft Design and Research Institute， Aviation Industry Corporation of China，Limited，Shenyang 110000，China
3.
Flying College，Binzhou University，Binzhou Shandong 256600，China

摘要

摘要:
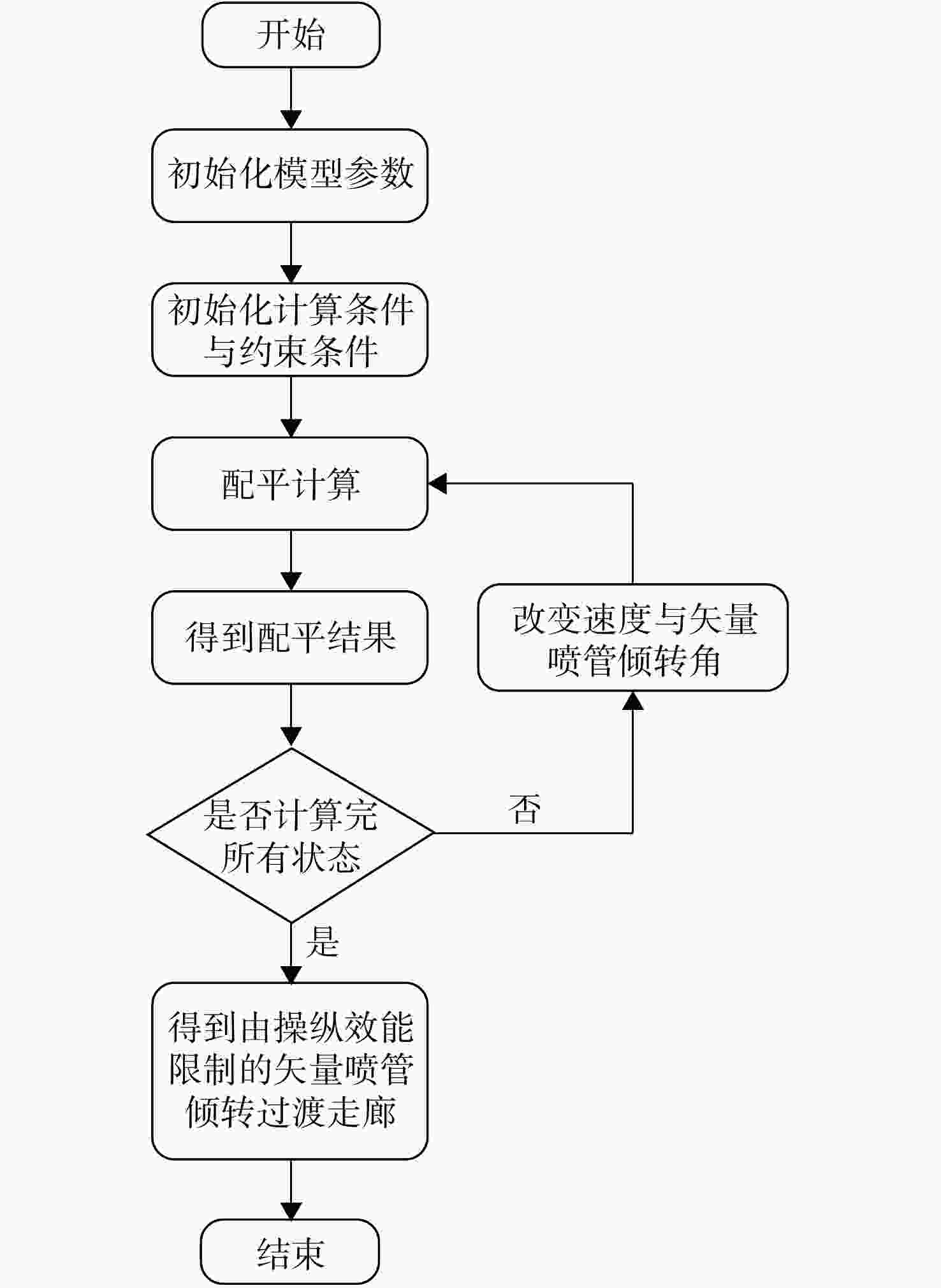
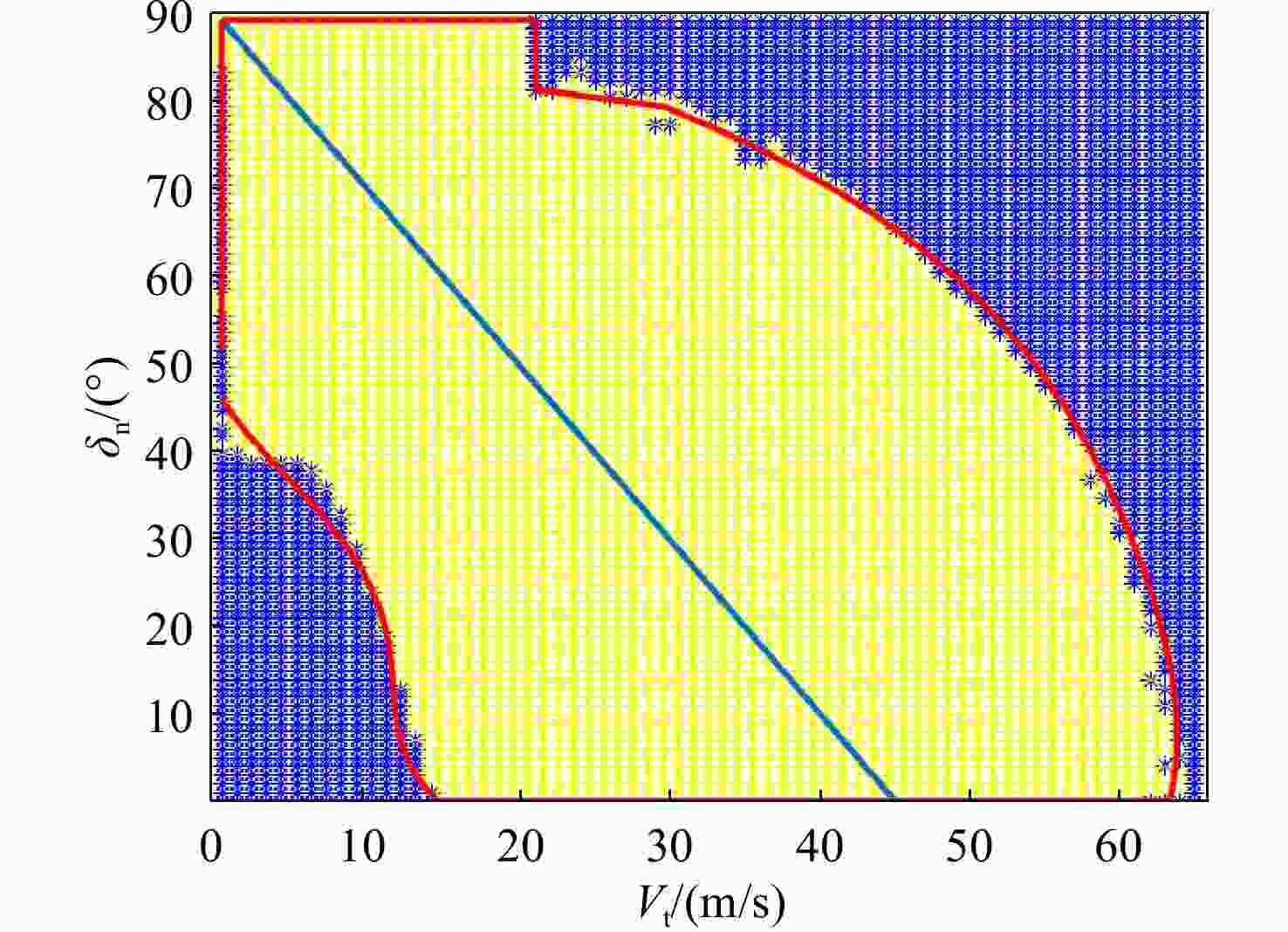
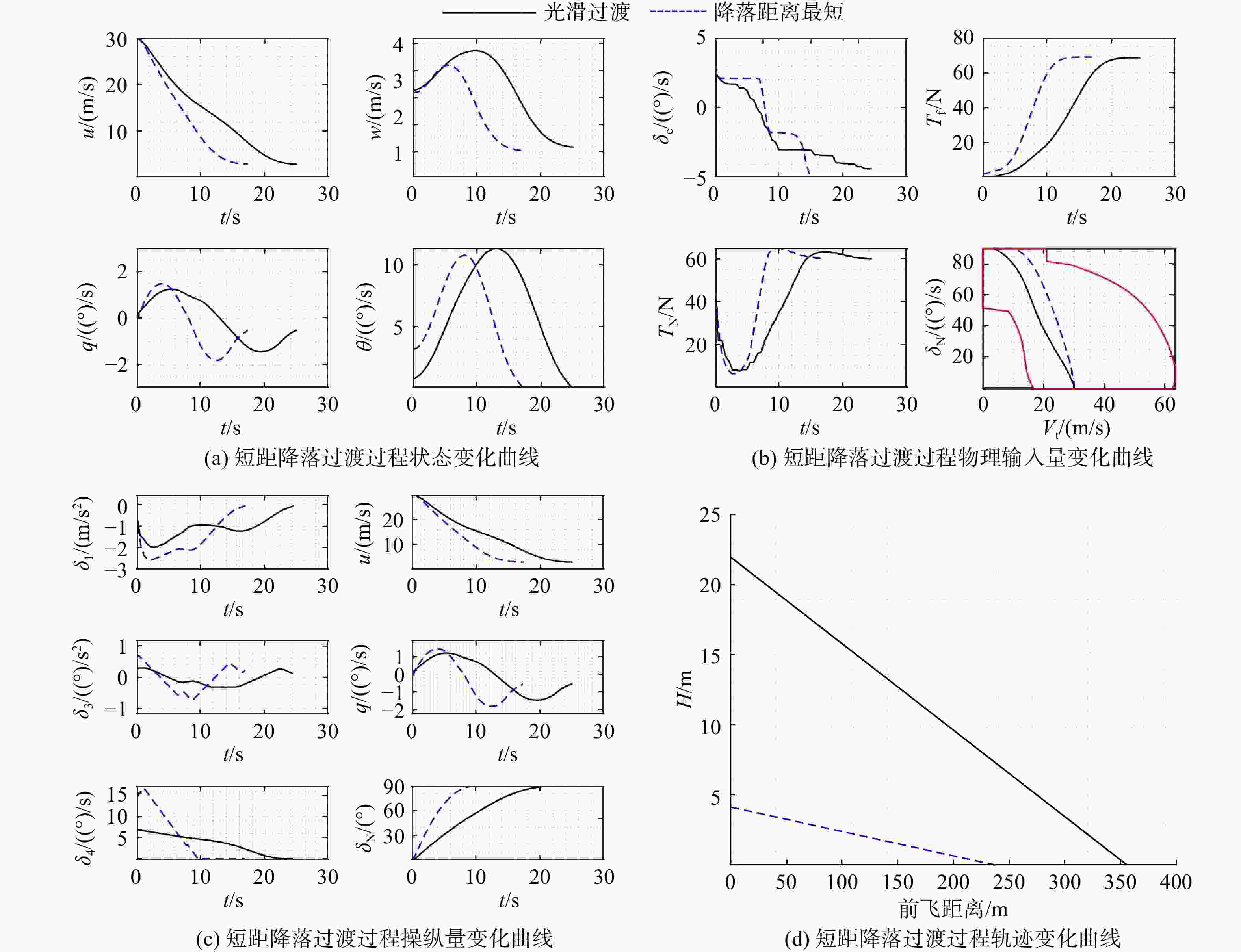
针对推力矢量型垂直/短距起降（vertical/short takeoff and landing, V/STOL）飞行器的动态过渡过程模型，综合考虑过渡走廊限制、操纵冗余及不同起降任务需求指标，研究最优过渡操纵策略。考虑V/STOL 飞行器的喷射气流效应，对飞行器进行全量动力学建模。利用可达平衡集方法，建立通用过渡走廊计算框架。设计了能够在V/STOL过渡段和高速飞行间平稳过渡的操纵方式。将推力矢量飞行器的动态倾转过渡过程转化为非线性动态最优控制问题，根据不同起降任务特点建立合理的指标和约束，采用直接转换法和序列二次规划算法进行求解，得出不同任务特点下的最优操纵策略与过渡过程。采用可达平衡集计算过渡走廊的方法，不仅不受飞行器类型的限制，更简化了构造过程，具有良好的通用性与鲁棒性。以光滑过渡为目标的优化结果使得飞行员在飞行器过渡过程中的操纵量变化大幅减小，从而使得飞行员能更加专注于对飞行器运动的操纵；以距离更短为目标的优化结果则使得降落过程的飞行距离缩短了30%左右。从操纵策略出发的优化结果使得驾驶员能够更好掌握操纵关注点及边界，增加了整个动态过渡过程的安全性。
- 推力矢量 /
- 动力学建模 /
- 过渡过程 /
- 过渡走廊 /
- 操纵策略 /
- 最优控制
Abstract:
For the dynamic tilting model of the vertical/short takeoff and landing (V/STOL) aircrafts during the transition process, a deep insight into the optimal control strategy was gained by considering the constraints of the conversion corridor, control redundancy and the demand indexes of different take-off/landing missions. Considering the jet-induced effect of the prototype aircraft, the V/STOL aircraft was totally modeled. A calculation architecture for the general conversion corridor was established based on the attainable balance set methodology. A control strategy was designed to ensure smooth conversion from the V/STOL aircraft transition process to the high-speed forward flight phase. By converting the dynamic tilting problem during the transition process to a dynamic nonlinear optimal control problem, the appropriate indexes and constraints were established according to the characteristics of different take-off/landing missions. The method of calculating the conversion corridor by reachable equilibrium set was not limited by the type of aircraft, but also was used to simplify the construction process with good versatility and robustness. The optimization results with the goal of smooth transition grealy reduced the pilot’s manipulation change during the aircraft transition process, so that the pilot can focus more on the manipulation of the aircraft motion. The optimization result for shorter distance shortened the flight distance of landing process by about 30%. The optimization results from the control strategy enabled the pilot to better grasp the control focus and boundary, and increased the safety of the entire dynamic transition process.
- thrust vector /
- dynamic modeling /
- transition process /
- conversion corridor /
- control strategy /
- optimal control

HTML

图 1 F-35B缩比模型图

Figure 1. Reduced ratio F-35B aircraft model

下载: 全尺寸图片幻灯片

图 2 动力系统纵向操纵原理

Figure 2. Longitudinal control principle of power system

下载: 全尺寸图片幻灯片

图 3 倾转过渡走廊计算流程

Figure 3. Computional flowchart for conversion corridor

下载: 全尺寸图片幻灯片

图 4 V/STOL飞行器的倾转过渡走廊

Figure 4. Conversion corridor of V/STOL aircraft

下载: 全尺寸图片幻灯片

图 5 短距起飞倾转过渡过程最优解

Figure 5. Optimal solution for tilting transition process of short take-off

下载: 全尺寸图片幻灯片

图 6 垂直起飞倾转过渡过程最优解

Figure 6. Optimal solution for tilting transition process of vertical take-off

下载: 全尺寸图片幻灯片

图 7 短距降落倾转过渡过程最优解

Figure 7. Optimal solution for tilting transition process of short landing

下载: 全尺寸图片幻灯片

表 1 缩比F35-B主要参数

Table 1. Main characteristics of reduced ratio F-35B

参数	数值
${d_{ {\text{tf} } } }/{\rm{m}}$	0.476
${d_{ {\text{tn} } } }/{\rm{m}}$	0.561
${x}_{0} /{\rm{m}}$	0.513
${\textit z}_{0} /{\rm{m} }$	0.100
${l}_{0}/{\rm{m}}$	0.141
${{\textit z}_{\text{n} } }/{\rm{m} }$	0.100

下载: 导出CSV

表 2 执行器饱和参数

Table 2. Actuator saturation parameters

参数	最大值
${\delta }_{ {\rm{e} } }/(\text{°})$	[−30, 30]
${T_{\text{f} } }/{\rm{N}}$	[0, 79.6]
${T_{\text{n} } }/{\rm{N}}$	[0, 79]
${\delta _{\text{n} } }/(\text{°})$	[0, 90]

下载: 导出CSV

表 3 全过程的操纵设计

Table 3. Whole process of control design

驾驶杆		油门杆	脚蹬	滚轮
纵向	横向	油门杆	脚蹬	滚轮
${ {\textit z}_{\rm{e}}}$轴速度	${y_{\rm{e}}}$轴速度	${x_{\rm{e}}}$轴速度	${ {\textit z}_{\rm{e}}}$轴角速度	矢量喷管倾转角速度（$ {\delta }_{4} $）
俯仰角加速度（$ {\delta }_{3} $）	滚转角速度	${x_{\rm{b}}}$轴加速度（$ {\delta }_{1} $）	方向舵
升降舵	副翼	矢量喷管推力	方向舵

下载: 导出CSV

表 4 约束参数

Table 4. Constraint parameters

参数	数值	参数	数值
$ t $	25	$ N $	46
$ {{\boldsymbol{\dot X}}_{\min }} $	[−5,−2,−5,−5]	$ {{\boldsymbol{\dot X}}_{\max }} $	[5,2,5,5]
$ {{\boldsymbol{\ddot X}}_{\min }} $	[−0.3,−0.3,−0.1,−0.8]	$ {{\boldsymbol{\ddot X}}_{\max }} $	[0.3,0.3,0.1,0.8]
$ {{\boldsymbol{\dot U}}_{\min }} $	[−3,−4,−5,−3]	$ {{\boldsymbol{\dot U}}_{\max }} $	[3,4,5,3]
$ {{\boldsymbol{\ddot U}}_{\min }} $	[−1,−1,−1,−0.5]	$ {{\boldsymbol{\ddot U}}_{\max }} $	[1,1,1,0.5]

下载: 导出CSV

参考文献(21)

[1]	SADDINGTON A J,KNOWLES K. A review of out-of-ground-effect propulsion-induced interference on STOVL aircraft[J]. Progress in Aerospace Sciences,2005,41(3): 175-191.
[2]	MARGASON R,ARLEDGE T,WARDWELL D,et al.Jet efflux characteristics and their influence on STOVL aircraft propulsion-induced effects[R].SAE Technical Paper 962250,1996.
[3]	BUCHHOLZ M D.Highlights of the JSF X-35 STOVL jet effects test effort[R].AIAA-2002-5962, 2002.
[4]	郑志成,周洲. 垂直起降飞机设计中升力风扇估算模型分析[J]. 飞行力学,2010,28(3): 21-23. doi: 10.13645/j.cnki.f.d.2010.03.006 ZHENG Zhicheng,ZHOU Zhou. Analysis of the estimation model of lift fan when designing VTOL[J]. Flight Dynamics,2010,28(3): 21-23. (in Chinese) doi: 10.13645/j.cnki.f.d.2010.03.006
[5]	KUHN R F,MARGASON R J,CURTIS P. Jet-induced effects the aerodynamics of jet-and fan-powered V/STOL aircraft in hover and transition[M].Reston, VA, US: AIAA, 2005: 13-52.
[6]	王向阳,朱纪洪,张义军. 推力矢量型V/STOL飞机动力学建模与分析[R].西安: 第三十二届中国控制会议,2013.
[7]	祝小平,王睿,周洲. 垂直起降固定翼飞翼布局无人机过渡飞行纵向稳定性研究[J]. 西北工业大学学报,2011,29(4): 548-553. doi: 10.3969/j.issn.1000-2758.2011.04.009 ZHU Xiaoping,WANG Rui,ZHOU Zhou. Longitudinal stability of vertical-take-off-and-landing (VTOL) fixed wing flying wing UAV during transitional flight[J]. Journal of Northwestern Polytechnical University,2011,29(4): 548-553. (in Chinese) doi: 10.3969/j.issn.1000-2758.2011.04.009
[8]	MAISEL M D,GIULIANETTI D J,DUGAN D C.The history of the XV-15 tilt rotor aircraft:from concept to flight[R].NASA SP-2000-4517,2000.
[9]	俞志明,陈仁良,孔卫红. 倾转四旋翼飞行器倾转过渡走廊分析方法[J]. 北京航空航天大学学报,2020,46(11): 2106-2113. YU Zhiming,CHEN Renliang,KONG Weihong. Analysis method for conversion corridor of quad tilt rotor aircraft[J]. Journal of Beijing University of Aeronautics and Astronautics,2020,46(11): 2106-2113. (in Chinese)
[10]	曹芸芸,陈仁良. 倾转旋翼飞行器发动机短舱倾转角度-速度包线分析[J]. 航空动力学报,2011,26(10): 2174-2180. CAO Yunyun,CHEN Renliang. Investigation on nacelle conversion envelope analysis method of tiltrotor aircraft[J]. Journal of Aerospace Power,2011,26(10): 2174-2180. (in Chinese)
[11]	夏青元,徐锦法,金开保. 倾转旋翼飞行器的建模和操纵分配策略[J]. 航空动力学报,2013,28(9): 2016-2028. XIA Qingyuan,XU Jinfa,JIN Kaibao. Tilt-rotor aircraft modeling and its manipulation assignment strategy[J]. Journal of Aerospace Power,2013,28(9): 2016-2028. (in Chinese)
[12]	TIAN Y,HE Y,LI X,et al.Simulation testing method of V/STOL flight control strategy[R].Beijing:the 10th World Congress on Intelligent Control and Automation,2012.
[13]	DENHAM J,PAINES J.Converging on a precision hover control strategy for the F-35B STOVL aircraft[R].AIAA-2008-6331,2008.
[14]	王洛烽,陈仁良,严旭飞. 直升机抛放吊挂后的最优操纵与分析[J]. 航空动力学报,2021,36(3): 543-552. WANG Luofeng,CHEN Renliang,YAN Xufei. Optimal control and analysis for helicopter after releasing slung load[J]. Journal of Aerospace Power,2021,36(3): 543-552. (in Chinese)
[15]	陈金鹤,汪正中,田洪源. 基于最优控制理论的倾转旋翼机跃障飞行仿真[J]. 西北工业大学学报,2020,38(6): 1266-1274. doi: 10.3969/j.issn.1000-2758.2020.06.016 CHEN Jinhe,WANG Zhengzhong,TIAN Hongyuan. Hurdle-hop simulation of tilt-rotor aircraft based on optimal control theory[J]. Journal of Northwestern Polytechnical University,2020,38(6): 1266-1274. (in Chinese) doi: 10.3969/j.issn.1000-2758.2020.06.016
[16]	严旭飞,陈仁良. 倾转旋翼机动态倾转过渡过程的操纵策略优化[J]. 航空学报,2017,38(7): 59-69. doi: 10.7527/S1000-6893.2017.520865 YAN Xufei,CHEN Renliang. Control strategy optimization of dynamic conversion procedure of tilt-rotor aircraft[J]. Acta Aeronautica et Astronautica Sinica,2017,38(7): 59-69. (in Chinese) doi: 10.7527/S1000-6893.2017.520865
[17]	程志强,朱纪洪,袁夏明,等. 推力矢量垂直短距飞机轨迹优化与控制[J]. 控制理论与应用,2020,37(1): 38-46. doi: 10.7641/CTA.2019.80515 CHENG Zhiqiang,ZHU Jihong,YUAN Xiaming,et al. Trajectory optimization and control design for transition of thrust-vectored vertical and/or short take-off and landing aircraft[J]. Control Theory and Applications,2020,37(1): 38-46. (in Chinese) doi: 10.7641/CTA.2019.80515
[18]	龚正. 先进飞行器非定常气动力建模、控制律设计及验证方法研究[D].南京:南京航空航天大学,2011. GONG Zheng.Research on unsteady aerodynamic modeling,control law design and clearance for advanced aerospace vehicle[D].Nanjing: Nanjing University of Aeronautics and Astronautics,2011.(in Chinese)
[19]	叶辉.推力矢量飞机过失速机动的鲁棒控制与边界保护[D].南京:南京航空航天大学,2016. YE Hui. Robust control and envelope protection for post-stall maneuver of TVC aircraft[D].Nanjing: Nanjing University of Aeronautics and Astronautics,2016. (in Chinese)
[20]	GOMAN M G,KHRAMTSOVSKY A V,KOLESNIKOV E N. Evaluation of aircraft performance and maneuverability by computation of attainable equilibrium sets[J]. Journal of Guidance,Control,and Dynamics,2008,31(2): 329-339. doi: 10.2514/1.29336
[21]	GILL P E,MURRAY W,SAUNDERS M A.User’s guide for SNOPT version 7: software for large-scale nonlinear programming[D].San Diego, US: University of California,2007.